福建省厦门市2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个数中，最小的数为（）

A、 $- 5$ B、 $- 4$ C、 $0$ D、 $1$

查看试题解析
2. 如图是某个几何体的展开图，该几何体是（）

A、三棱锥 B、三棱柱 C、圆柱 D、圆锥

查看试题解析
3. 多项式 $2 x^{3} - x^{2} + x - 1$ 的次数是（）

A、 $6$ B、 $5$ C、 $4$ D、 $3$

查看试题解析
4. 如图，射线 $O A$ 表示的方向是（）

A、北偏东 $65 °$ B、北偏西 $35 °$ C、南偏东 $65 °$ D、南偏西 $35 °$

查看试题解析
5. 下列 $4$ 个生产、生活现象中，可用“两点之间线段最短”来解释的是（）

A、用两根钉子就可以把木条固定在墙上 B、植树时，只要选出两棵树的位置，就能确定同一行树所在的直线 C、把弯曲的公路改直，就能缩短路程 D、砌墙时，经常在两个墙角的位置分别插一根木桩拉一条直的参照线

查看试题解析
6. 已知 $x^{3 - m - n} y^{2}$ 与 $2 x y^{2}$ 是同类项，则m，n可以是（）

A、 $1$ ， $0$ B、 $- 1$ ， $3$ C、 $- 2$ ， $1$ D、 $- 3$ ， $1$

查看试题解析
7. a，b是有理数，它们在数轴上对应点的位置如图所示，把a，-a，b，-b按照从小到大的顺序排列，正确的是（）

A、 $a < - b < b < - a$ B、 $- b < a < - a < b$ C、 $a < - a < b < - b$ D、 $- a < a < - b < b$

查看试题解析
8. 已知有理数a与b互为相反数，b与c互为倒数，下列等式错误的是（）

A、 $b c = 1$ B、 $\frac{a}{b} = - 1$ C、 $a c = - 1$ D、 $\frac{a}{c} = - 1$

查看试题解析
9. 如图，线段AB上有C，D两点，以AC，CD，BD为直径的圆的周长分别是 $C_{1}$ 、 $C_{2}$ 、 $C_{3}$ ，以AB为直径的圆的周长为C，下列结论正确的是（）

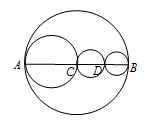A、 $C_{1}$ ＋ $C_{2}$ ＝C＋ $C_{3}$ B、 $C_{1}$ ＋ $C_{2}$ ＋ $C_{3}$ ＝C C、 $C_{1}$ ＋ $C_{2}$ ＋ $C_{3}$ ＞C D、 $C_{1}$ ＋ $C_{2}$ ＋ $C_{3}$ ＜C

查看试题解析
10. 小宇同学喜欢玩“数字游戏”，他将 $1$ ， $2$ ， $3$ ，……， $100$ 这 $100$ 个数按照下表进行排列，每行 $7$ 个数，从左到右依次大 $1$ ．若在下表中，移动带阴影的框，框中的 $4$ 个数的和可以是（）

A、 $42$ B、 $214$ C、 $254$ D、 $390$

查看试题解析

二、填空题

11. 计算下列各题：
⑴ $- 1 + 6 =$ ；（2） $3 - 5 =$ ；（3） $- 2 \times (- 5) =$ ；

⑷ $- 12 \div 1.5 =$ ；（5） $- 2^{4} \div 8 =$ ；（6） ${(- 1)}^{2 n + 9} + | - 3 | =$ ；

查看试题解析
12. 厦门市轨道交通 $2$ 号线工程起点位于天竺山森林公园山脚下，终点是五缘湾，全长约 $41600$ 米．将 $41600$ 用科学记数法表示为．

查看试题解析
13. 若 $∠ A = 59.6 °$ ，则它的余角为 $°$ '．

查看试题解析
14. 若 $x = - 2$ 是关于x的方程 $2 x + 5 a = 6$ 的解，则 $a =$ ．

查看试题解析

15. 下表是某中学足球冠军杯第一阶段A组赛不完整的积分表．A组共

4

个队，每个队分别与其它

3

个队进行主客场比赛各一场，即每个队都要进行

6

场比赛．每队每场比赛积分都是自然数．（总积分

=

胜场积分

+

平场积分

+

负场积分）

球队	比赛场次	胜场次数	平场次数	负场次数	总积分
战神队	$6$	$3$	$2$	$1$	$11$
旋风队	$6$		$2$		$2$
龙虎队	$6$	$2$	$3$	$1$	$9$
梦之队	$6$			$2$

本次足球小组赛中，平一场积分，梦之队总积分是分．

查看试题解析

16. 如图，射线 $O C$ ， $O D$ 在 $∠ A O B$ 内， $∠ A O B$ 和 $∠ B O C$ 互为补角 $∠ B O D = \frac{1}{3} ∠ A O B$ ，若 $∠ C O D$ 比 $∠ B O D$ 大 $m °$ （ $m < 30$ ），则 $∠ A O C =$ $°$ （用含m的式子表示）

查看试题解析

三、解答题

17.

(1)、计算： $4 \div 2 \times (- 3) - (- 9)$ ；

(2)、计算： $x + (2 x - 2) - (3 x + 5)$ ；

(3)、计算： $[{(- 2)}^{3} + (3^{2} - 5) \times 2] \div (- \frac{1}{3})$ ；

(4)、解方程： $5 y + 9 = 3 y - 1$ ．

查看试题解析
18. 先化简，再求值： $5 x^{2} - 3 (2 x^{2} + 4 y) + 2 (x^{2} - y)$ ，其中 $x = - 2$ ， $y = \frac{1}{7}$ ．

查看试题解析
19. 当x取何值时， $\frac{x + 1}{2}$ 和 $\frac{4 - x}{4}$ 的值相等？

查看试题解析
20. 如图，已知 $∠ A O B = 128 °$ ， $O C$ 平分 $∠ A O B$ ，请你在 $∠ C O B$ 内部画射线 $O D$ ，使 $∠ C O D$ 和 $∠ A O C$ 互余，并求 $∠ C O D$ 的度数．

查看试题解析
21. 《孙子算经》是中国传统数学的重要著作，其中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根木头的长，绳子还剩余 $4.5$ 尺；将绳子对折再量木头，则木头还剩余 $1$ 尺，问木头长多少尺？请你用一元一次方程的知识解决．

查看试题解析
22. 借助有理数的运算，对任意有理数a，b，定义一种新运算“ $\oplus$ ”规则如下： $a \oplus b = | a + b |$ 例如， $2 \oplus (- 1) = | 2 + (- 1) | = 1$ ．

(1)、求 $[5 \oplus (- 2)] \oplus 4$ 的值；

(2)、我们知道有理数加法运算具有交换律和结合律，请你探究这种新运算“ $\oplus$ ”是否也具有交换律和结合律？若具有，请说明理由；若不具有，请举一个反例说明．

查看试题解析

23. 某市从

2019

年

1

月

1

日开始实施阶梯电价制，居民生活用电价格方案如下：

档次	月用电量		电价（单位：元 $/$ 度）
档次	春秋季（ $3$ ， $4$ ， $5$ ， $9$ ， $10$ ， $11$ 月）	冬夏季（ $1$ ， $2$ ， $6$ ， $7$ ， $8$ ， $12$ 月）	电价（单位：元 $/$ 度）
第 $1$ 档	不超过 $200$ 度的部分	不超过 $200$ 度的部分	$0.5$
第 $2$ 档	超过 $200$ 度但不超过 $350$ 度的部分	超过 $200$ 度但不超过 $450$ 度的部分	$0.55$
第 $3$ 档	超过 $350$ 度的部分	超过 $450$ 度的部分	$0.8$

例：若某用户 $2019$ 年 $6$ 月的用电量为 $300$ 度，则需交电费为：

$200 \times 0.5 + (300 - 200) \times 0.55 = 155$ （元）．

(1)、若小辰家

2019

年

5

月的用电量为

400

度，则需交电费多少元？

(2)、若小辰家

2019

年

8

月和

9

月用电量相同，共交电费

660

元，问小辰家

8

月份用多少度电？

查看试题解析

24. 如图，点C在线段 $A B$ 上， $O$ 是线段 $B C$ 的中点．

(1)、在线段 $CO$ 上，求作点E，使 $C E = 2 A C$ ．
（要求：尺规作图，不写作法保留作图痕迹）

(2)、在（1）的条件下， $A B = 12$ ，
①若 $B O = 2 E O$ ，求 $A C$ 的长；

②若点D在线段 $B O$ 上，且 $2 O D = 9 A C - 12$ ，请你判断点E是哪条线段的中点，并说明理由．

查看试题解析
25. 如图，已知 $∠ A O C = 90 °$ ， $∠ B O C = 2 ∠ A O B$ ，射线 $O M$ 绕点O从射线 $O A$ 位置开始按顺时针方向以每秒 $4 °$ 的速度旋转，到 $O C$ 停止；同时射线 $O N$ 绕点O从射线 $O C$ 位置开始按逆时针方向以每秒 $5 °$ 的速度旋转．

设当旋转时间为t秒时， $∠ M O N$ 为 $m °$ （ $m < 90$ ）．

(1)、填空：当t=3秒，求m=；

(2)、若 $m = 10.8$ ，且 $t < 10$ 时，求t的值；

(3)、若射线 $O N$ 旋转到 $O B$ 后立即返回，按顺时针方向旋转，到 $O C$ 停止．用含t的式子表示m．

查看试题解析