福建省莆田市2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-11-16 类型:期末考试
一、单选题
-
1. 2020的相反数是( )A、 2020 B、﹣2020 C、 D、﹣2. “中国计划2020年发射火星探测器,争取2021年到达火星.”2016年3月4日,中国政协委员、航天专家叶培建的这个消息让许多中国人感到振奋.已知地球到火星的最近距离约为55000000公里,将55000000这个数用科学记数法表示为( )A、 B、 C、 D、3. 下列各组中的两个单项式,属于同类项的是( )A、 与a B、 与 C、 与 D、a与b4. 下列图形中可以作为一个三棱柱的展开图的是( )A、
 B、
B、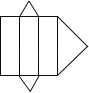 C、
C、 D、
D、 5. 如图,点A的方向是位于点O的( )
5. 如图,点A的方向是位于点O的( ) A、北偏东 B、北偏东 C、南偏东 D、南偏东6. 我国古代名著《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四,问人数几何?原文意思是:现在有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问共有多少人?如果假设共有 人,则可列方程为( )A、 B、 C、 D、7. 下列语句错误的是( )A、同角的余角相等 B、两点确定一条直线 C、连接两点间的线段叫做两点间的距离 D、两点之间,线段最短8. 已知等式 ,则下列等式中不一定成立的是( )A、 B、 C、 D、9. 若四个互不相等的整数的积为6,那么这四个整数的和是( )A、-1或5 B、1或-5 C、-5或5 D、-1或110. 如图,数轴上A、B、C三点所表示的数分别为a、b、c,满足 且 .那么下列各式正确的是( )
A、北偏东 B、北偏东 C、南偏东 D、南偏东6. 我国古代名著《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四,问人数几何?原文意思是:现在有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问共有多少人?如果假设共有 人,则可列方程为( )A、 B、 C、 D、7. 下列语句错误的是( )A、同角的余角相等 B、两点确定一条直线 C、连接两点间的线段叫做两点间的距离 D、两点之间,线段最短8. 已知等式 ,则下列等式中不一定成立的是( )A、 B、 C、 D、9. 若四个互不相等的整数的积为6,那么这四个整数的和是( )A、-1或5 B、1或-5 C、-5或5 D、-1或110. 如图,数轴上A、B、C三点所表示的数分别为a、b、c,满足 且 .那么下列各式正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:12. 已知关于x的方程 的解是 ,则a的值是 .13. 计算: .14. 已知 ,则 的值为 .15. 如图,点E,F分别在长方形ABCD的边AD,CD上,连接BE.将长方形 沿 对折,点A落在 处;将 对折,点D落在 的延长线上的 处,得到折痕 .若 ,则 .
 16. 如图所示,用3根火柴可拼成1个三角形,5根火柴可拼成2个三角形,7根火柴可拼成3个三角形……,按这个规律拼,用99根火柴可拼成个三角形.
16. 如图所示,用3根火柴可拼成1个三角形,5根火柴可拼成2个三角形,7根火柴可拼成3个三角形……,按这个规律拼,用99根火柴可拼成个三角形.
三、解答题
-
17. 计算:(1)、(2)、18. 解方程:(1)、(2)、19. 如图,已知三点A,B,C,请按照下列语句作图.(保留作图痕迹)
 (1)、作射线 ;(2)、连接 并延长 到D,使得 .20. 先化简,再求值: ,其中 , .21. 如图,点B为线段 的中点,点C在线段 上,且 ,若 ,求 的长.
(1)、作射线 ;(2)、连接 并延长 到D,使得 .20. 先化简,再求值: ,其中 , .21. 如图,点B为线段 的中点,点C在线段 上,且 ,若 ,求 的长. 22. 如图是某长方体的展开图,它的棱长如图所示,请计算原长方体的表面积和体积.(结果用含a的式子表示)
22. 如图是某长方体的展开图,它的棱长如图所示,请计算原长方体的表面积和体积.(结果用含a的式子表示) 23. 为了发展校园足球运动,某城区五校决定联合购买一批足球服和足球.经过市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球服和足球,已知每套足球服比每个足球多60元,两套足球服与三个足球的费用相等.经洽谈,甲商场的优惠方案是:每购买20套足球服,送一个足球;乙商场的优惠方案是:若购买足球服超过80套,则购买的足球打八折,若购买足球服不超过80套,不打折.(1)、求每套足球服和每个足球的价格各是多少元;(2)、若城区五校联合购买120套足球服和a( )个足球,假如你是本次购买任务的负责人,你会选择到甲、乙两家中的哪一家商场购买更便宜?请说明理由.24. 如图,在三角形 中, , , .点P从点A出发以2个单位长度/秒的速度沿 的方向运动,点Q从点B沿 的方向与点P同时出发;当点P第一次回到A点时,点P,Q同时停止运动;用t(秒)表示运动时间.
23. 为了发展校园足球运动,某城区五校决定联合购买一批足球服和足球.经过市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球服和足球,已知每套足球服比每个足球多60元,两套足球服与三个足球的费用相等.经洽谈,甲商场的优惠方案是:每购买20套足球服,送一个足球;乙商场的优惠方案是:若购买足球服超过80套,则购买的足球打八折,若购买足球服不超过80套,不打折.(1)、求每套足球服和每个足球的价格各是多少元;(2)、若城区五校联合购买120套足球服和a( )个足球,假如你是本次购买任务的负责人,你会选择到甲、乙两家中的哪一家商场购买更便宜?请说明理由.24. 如图,在三角形 中, , , .点P从点A出发以2个单位长度/秒的速度沿 的方向运动,点Q从点B沿 的方向与点P同时出发;当点P第一次回到A点时,点P,Q同时停止运动;用t(秒)表示运动时间. (1)、当t为多少时,P是 的中点;(2)、若点Q的运动速度是 个单位长度/秒,是否存在t的值,使得 ;(3)、若点Q的运动速度是a个单位长度/秒,当点P,Q是 边上的三等分点时,求a的值.25. 定义:若 ,且 ,则我们称 是 的差余角.例如:若 ,则 的差余角 .
(1)、当t为多少时,P是 的中点;(2)、若点Q的运动速度是 个单位长度/秒,是否存在t的值,使得 ;(3)、若点Q的运动速度是a个单位长度/秒,当点P,Q是 边上的三等分点时,求a的值.25. 定义:若 ,且 ,则我们称 是 的差余角.例如:若 ,则 的差余角 .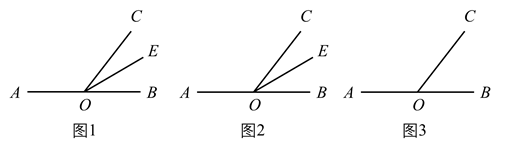 (1)、如图1,点O在直线 上,射线 是 的角平分线,若 是 的差余角,求 的度数.(2)、如图2,点O在直线 上,若 是 的差余角,那么 与 有什么数量关系.(3)、如图3,点O在直线 上,若 是 的差余角,且 与 在直线 的同侧,请你探究 是否为定值?若是,请求出定值;若不是,请说明理由.
(1)、如图1,点O在直线 上,射线 是 的角平分线,若 是 的差余角,求 的度数.(2)、如图2,点O在直线 上,若 是 的差余角,那么 与 有什么数量关系.(3)、如图3,点O在直线 上,若 是 的差余角,且 与 在直线 的同侧,请你探究 是否为定值?若是,请求出定值;若不是,请说明理由.