福建省宁德市2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，比﹣2小的数是（）

A、﹣3 B、﹣1 C、0 D、1

查看试题解析
2. 单项式 $- \frac{1}{3} a^{3} b$ 的系数是（）

A、 $- 1$ B、 $- \frac{1}{3}$ C、 $\frac{1}{3}$ D、4

查看试题解析
3. 为庆祝新中国成立70周年，天安门广场举行盛大国庆阅兵仪式，参加这次阅兵的有59个方队和联合军乐团，总规模约15 000人．将15 000用科学记数法表示为（）

A、0.15 ×10⁵ B、1.5×10⁴ C、15×10³ D、1.5×10⁵

查看试题解析
4. 要清楚地反映近几日气温的变化情况，最适合制作的是（）

A、折线统计图 B、扇形统计图 C、频数直方图 D、频数分布表

查看试题解析
5. 如图，将一个直角三角形绕它的一条直角边所在的直线旋转一周，得到的几何体是（）

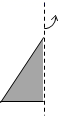A、长方体 B、球 C、圆柱 D、圆锥

查看试题解析
6. 下列运算正确的是（）

A、 $3 a + b = 3 a b$ B、 $3 a^{2} - 2 a^{2} = a^{2}$ C、 $3 (a - 1) = 3 a - 1$ D、 $- (a - 1) = - a - 1$

查看试题解析
7. 下列调查中，适宜采用抽样调查的是（）

A、对飞机零部件质量的调查 B、对全班45位同学身高的调查 C、对动车站客流量的调查 D、对全运会运动员使用兴奋剂的调查

查看试题解析
8. 关于 3⁵ 的意义，描述正确的是（）

A、表示5个3相加 B、表示3个5相加 C、表示5个3相乘 D、表示3个5相乘

查看试题解析
9. 对有理数运算的描述，下列说法错误的是（）

A、同号两数相加，取相同的符号，并把绝对值相加 B、减去一个数，等于加上这个数的相反数 C、两数相乘，同号得正，异号得负，并把绝对值相乘 D、除以一个数等于乘这个数的绝对值

查看试题解析
10. 在课题学习中，老师要求用长为12厘米，宽为8厘米的长方形纸片制作一个无盖的长方体纸盒．三位同学分别以下列方式在长方形纸片上截去两角（图中阴影部分），然后沿虚线折成一个无盖的长方体纸盒．
甲：如图1，盒子底面的四边形ABCD是正方形；

乙：如图2，盒子底面的四边形ABCD是正方形；

丙：如图3，盒子底面的四边形ABCD是长方形，AB=2AD．

将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列，正确的是

A、甲＞乙＞丙 B、甲＞丙＞乙 C、丙＞甲＞乙 D、丙＞乙＞甲

查看试题解析

二、填空题

11. 12的相反数是；的相反数是﹣2 $\frac{3}{4}$ ；﹣ $\frac{2}{3}$ 的绝对值是．

查看试题解析
12. 由 $3 x = 2 x - 1$ 得 $3 x - 2 x = - 1$ ，在此变形中，方程两边同时．

查看试题解析
13. 某班学生参加学校组织的“垃圾分类”知识竞赛，将学生成绩制成如图所示的频数分布直方图(每组数据包括左端值不包括右端值)，其中成绩为“优良”（80分及80分以上）的学生有人．

查看试题解析
14. 比较两个角的大小关系：小明用度量法测得∠AOB=45°，∠COD=50°；小丽用叠合法比较，将两个角的顶点重合，边OB与OD重合，边OA和OC置于重合边的同侧，则边OA ．（填序号：①“在∠COD的内部”；②“在∠COD的外部”；③“与边OC重合” )

查看试题解析
15. 如图，是一个数值转换机，若输入的数为5，则输出的数是．

查看试题解析
16. 若线段A₁A₂=1，在线段A₁A₂的延长线上取一点A₃ ，使A₂是A₁A₃的中点；在线段A₁A₃的延长线上取一点A₄ ，使A₃是A₁A₄的中点；在线段A₁A₄的延长线上取一点A₅ ，使A₄是A₁A₅的中点……，按这样操作下去，线段A₁A₂₀₂₀= ．

查看试题解析

三、解答题

17. 计算：

(1)、 $- 1^{2} - 3 \div \frac{1}{4} - (- 2)$ ；

(2)、 $| - 18 | \times (\frac{1}{2} - \frac{5}{6} + \frac{2}{3})$ ；

(3)、 $\frac{3}{2} a^{2} b - \frac{1}{2} a b - \frac{3}{2} (a^{2} b - a b)$ ．

查看试题解析
18. 解方程： $2 + \frac{5 x - 1}{2} = x$ ．

查看试题解析
19. 如图，∠COD=45°，∠BOD= $\frac{1}{3}$ ∠COD，OC是∠AOB的平分线，求∠AOD的度数．

查看试题解析
20. 春节前，由35名同学组成的志愿者小分队，共制作了180个纸灯笼送给敬老院．平均每名男生制作4个，每名女生制作6个．求男生、女生各多少名．

查看试题解析
21. 如图，用10个大小相同的小立方块搭成一个组合体．

⑴请在指定位置画出该组合体从左面、上面看到的形状图；

⑵在不改变该组合体中小立方块个数的前提下，从中移动一个小立方块，使所得新组合体与原组合体相比，从左面、上面看到的形状图保持不变，但从正面看到的形状图改变了，请画出新组合体从正面看到的所有可能的形状图．（所给的方格图不一定全用，不够可添）

查看试题解析
22. 在精准扶贫政策的扶持下，贫困户老李今年试种的百香果获得大丰收，共收获2 000千克．扶贫小组帮助他将百香果按照品质从高到低分成A，B，C，D，E五个等级，并根据数据绘制了如下的扇形统计图和频数分布表：

请根据图表信息解答下列问题：

(1)、m=；n=；a=；

(2)、求扇形统计图中“E”所对应的圆心角的度数；

(3)、为了帮助贫困户老李销售百香果，扶贫小组联系了甲、乙两位经销商．他们分别给出如下收购方案：
甲：全部按5元/千克收购；

乙：按等级收购：C等级单价为6.5元/千克，每提高一个等级单价提高1元/千克，剩下的D，E两个等级单价均为2元/千克．

请你通过计算，判断哪个经销商的方案使老李盈利更多．

查看试题解析
23. 如图，在数轴上点A所表示的数是 $- 5$ ，点B在点A的右侧，AB=6；点C在AB之间， AC=2BC．

(1)、在数轴上描出点B；

(2)、求点C所表示的数，并在数轴上描出点C；

(3)、已知在数轴上存在点P，使PA+PC=PB，求点P所表示的数．

查看试题解析