福建省南平市2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 若有理数a与3互为相反数，则a的值是（）.

A、3 B、－3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 2019年10月1日新中国成立70周年．央视新闻与快手合作推出“1+6”国庆阅兵多链路直播间，总观看人次突破5.13亿．将数据用513000000科学记数法表示为（）

A、 $51.3 \times 10^{7}$ B、 ${5.13}^{8}$ C、 $5.13 \times 10^{8}$ D、 $513 \times 10^{6}$

查看试题解析
3. 从三个不同方向看一个几何体，得到的平面图形如图所示，则这个几何体是（）

A、长方体 B、圆锥 C、圆柱 D、球

查看试题解析
4. 在数轴上有两个点A、B ，点A表示-3，点B与点A相距5个单位长度，则点B表示的数为（）.

A、-2或8 B、2或-8 C、-2 D、-8

查看试题解析
5. 下列说法正确的是（）

A、单项式 $\frac{3 x y^{2}}{5}$ 的系数是 $3$ B、多项式 $2 x^{2} - 3 y^{2} + 5 x y^{2}$ 是三次三项式 C、单项式 $- 2^{2} m^{4} n$ 的次数是 $7$ D、单项式 $2 a^{2} b$ 与 $a b^{2}$ 是同类项

查看试题解析
6. 已知 $∠ A = 115 °$ ， $∠ B$ 是 $∠ A$ 的补角，则 $∠ B$ 的余角的度数是（）

A、 $65 °$ B、 $115 °$ C、 $15 °$ D、 $25 °$

查看试题解析
7. 下列各等式的变形中，一定正确的是（）

A、若 $\frac{a}{2} = 0$ ，则 $a = 2$ B、若 $a = b$ ，则 $2 (a - 1) = 2 (b - 1)$ C、若 $- 2 a = - 3$ ，则 $a = \frac{2}{3}$ D、若 $a = b$ ，则 $\frac{a}{2 c} = \frac{b}{2 c}$

查看试题解析
8. 有理数a，b在数轴上所对应的点的位置如图，下列说法正确的是（）

A、 $a > b$ B、 $- b < - 1$ C、 $- a < b$ D、 $| - b | < | a |$

查看试题解析
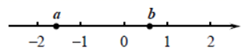9. 我国明朝珠算发明家程大位，他完成的古代数学名著《直指算法统宗》，详述了传统的珠算规则，确立了算盘用法．书中记载如下问题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁．意思是：有 $100$ 个和尚分 $100$ 个馒头，如果大和尚 $1$ 人分 $3$ 个，小和尚 $3$ 人分 $1$ 个，正好分完，大、小和尚各有多少人？设大和尚有 $x$ 人，则可列方程为（）

A、 $3 x + \frac{1}{3} (100 - x) = 100$ B、 $3 x + 3 (100 - x) = 100$ C、 $\frac{1}{3} x + 3 (100 - x) = 100$ D、 $x + \frac{1}{3} (100 - x) = 100$

查看试题解析
10. 如图 $3 \times 3$ 网格中，每一横行、每一竖列以及两条斜对角线上的三个数的和都相等，则 $b - a$ 的值是（）

A、 $- 3$ B、 $- 2$ C、 $2$ D、 $3$

查看试题解析

二、填空题

11. 计算： $| - 3 | - 5 =$ ．

查看试题解析
12. 方程 $x^{n + 2} = 7$ 是关于x的一元一次方程，则 $n =$ ．

查看试题解析
13. 如图，点C在线段 $A B$ 上，且 $A C = \frac{1}{3} A B$ ，点D在线段 $B C$ 上， $A D = 5$ ， $B D = 3$ ，则线段 $C D$ 的长度为．

查看试题解析
14. 如图，甲从A出发沿着北偏东 $60 °$ 方向走到B的位置，乙从A出发沿着南偏西 $23 °$ 方向走到C的位置，则 $∠ C A B$ 的度数为．

查看试题解析
15. 已知 $∠ A O B = 45 °$ ， $∠ B O C = 27 °$ ，则 $∠ A O C =$ ．

查看试题解析
16. 若 $n_{1} = 1 - \frac{2}{3}$ ， $n_{2} = 1 - \frac{1}{n_{1}}$ ， $n_{3} = 1 - \frac{1}{n_{2}}$ ， $n_{4} = 1 - \frac{1}{n_{3}}$ ， $\dots$ ，则 $n_{2020} =$ ．

查看试题解析

三、解答题

17. 计算： $- 2^{2} \div \frac{9}{4} \times \frac{2}{3}$ ．

查看试题解析
18. 先化简，再求值： $m^{2} + 2 m n - 2 (3 m^{2} - m n)$ ，其中 $m = - 1$ ， $n = 2$ .

查看试题解析
19. 解方程： $\frac{1 - 2 x}{2} + 3 = \frac{x + 2}{4}$ ．

查看试题解析
20. （尺规作图）如图，已知直线l和直线外三点A，B，C，按下列要求作图：

⑴作射线 $A B$ ，连接 $B C$ ；

⑵反向延长 $B C$ 至D，使得 $B D = B C$ ；

⑶在直线l上确定点E，使得 $A E + C E$ 最小．

请说明作图依据：．

查看试题解析
21. 如图，已知∠AOB=90°，∠EOF=60°，OE平分∠AOB，OF平分∠BOC，求∠COB和∠AOC的度数．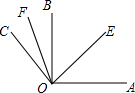

查看试题解析
22. 某超市销售某品牌的羽毛球拍和乒乓球拍，羽毛球拍每副定价 $80$ 元，乒乓球拍每副定价 $20$ 元．店庆期间该超市开展促销活动，活动期间向顾客提供两种优惠方案．
方案一：买一副羽毛球拍送一副乒乓球拍；

方案二：羽毛球拍和乒乓球拍都按定价的 $90 %$ 付款．

现某校要到该超市购买羽毛球拍 $5$ 副，乒乓球拍x副（ $x > 5$ ）

(1)、若该校按方案一购买，需付款元；（用含x的代数式表示），若该校按方案二购买，需付款元．（用含x的代数式表示）

(2)、当x取何值时，两种方案一样优惠？

(3)、当 $x = 20$ 时，通过计算说明此时按哪种方案购买较为合算？你能给出一种更为省钱的购买方法吗？请写出你的购买方法，并计算需付款多少元？

查看试题解析
23. 已知数轴上两点A，B（点B在点A的右侧），若数轴上存在一点C，使得 $A C = 2 B C$ ，则称点C为点A，B的“ $2$ 倍分点”，若使得 $A C = 3 B C$ ，则称点C为点A，B的“ $3$ 倍分点”， $\dots$ ，若使得 $A C = k B C$ ，则称点C为点A，B的“k倍分点（k为正整数）．请根据上述规定回答下列问题：

(1)、如图，若点A表示数 $- 1$ ，点B表示数 $2$ ．
①当点C表示数 $1$ 时，则 $k =$ ；

②当点C为点A，B的“ $5$ 倍分点”时，求点C表示的数；

(2)、若点A表示数a， $A B = 6$ ，当点C为 $A B$ 的“ $3$ 倍分点”时，请直接写出点C表示的数．（用含a的代数式表示）

查看试题解析