福建省龙岩市新罗区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 2020的相反数是（）

A、 2020 B、﹣2020 C、 $\frac{1}{2020}$ D、﹣ $\frac{1}{2020}$

查看试题解析
2. 下图中的几何体从正面看能得到（）

A、 B、 C、 D、

查看试题解析
3. “一带一路”的“朋友圈”究竟有多大？“一带一路”涉及沿线65个国家，总涉及人口约4500000000，将4500000000用科学记数法表示为（　　）

A、4.5×10⁷ B、45×10⁸ C、4.5×10⁹ D、0.45×10¹⁰

查看试题解析
4. 下列运算正确的是（）

A、3m+3n＝6mn B、4x³﹣3x³＝1 C、﹣xy+xy＝0 D、a⁴+a²＝a⁶

查看试题解析
5. 下列说法错误的是（）

A、两条射线组成的图形叫角 B、两点之间线段最短 C、两点确定一条直线 D、0是单项式

查看试题解析
6. 如图，点C是线段AB上的点，点D是线段BC的中点，若AB=16cm，AC=10cm，则线段CD的长是（）

A、1cm B、2cm C、3cm D、4cm

查看试题解析
7. 把两块三角板按如图所示那样拼在一起，那么∠ABC的度数是（）

A、120° B、125° C、130° D、135°

查看试题解析
8. 运用等式性质进行的变形，正确的是( )

A、如果a=b，那么a+c=b-c； B、如果 $\frac{a}{c} = \frac{b}{c}$ ，那么a=b； C、如果a=b，那么 $\frac{a}{c} = \frac{b}{c}$ ； D、如果 $a^{2}$ =3a，那么a=3

查看试题解析
9. 已知a，b是有理数，若a在数轴上的对应点的位置如图所示，且a+b<0，则正确的结论是（）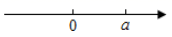

A、a>-b B、 $\frac{b}{a} < - 1$ C、b-a>0 D、 $| -a | > - b$

查看试题解析
10. 若a=-2020，则式子 $| a^{2} + 2019 a + 1 | + | a^{2} + 2021 a - 1 |$ 的值是（）

A、4036 B、4038 C、4040 D、4042

查看试题解析

二、填空题

11. 比较大小：-5-4（填“>”、“<”或“=”）．

查看试题解析
12. 如果向银行存入30000元记作+30000元，则从银行取出1500元记作元．

查看试题解析
13. 用四舍五入法，把数4.816精确到百分位，得到的近似数是．

查看试题解析
14. 如图是一个正方体的表面展开图，则原正方体中“喜”面所对面上的字是．

查看试题解析
15. 若 $4 x^{2} y^{3} + 2 a x^{2} y^{3} = 4 b x^{2} y^{3}$ ，则2+a-2b= ．

查看试题解析
16. 任何一个无限循环小数都可以写成分数的形式，应该怎样写呢？我们以无限循环小数 $0. \overset{•}{7}$ 为例进行说明：设 $0. \overset{•}{7}$ =x，由 $0. \overset{•}{7}$ =0.777……，可知，10x=7.7777……，所以10x-x=7，解方程，得 $x = \frac{7}{9}$ ，于是，得 $0. \overset{•}{7}$ = $\frac{7}{9}$ ，将 $0. \overset{•}{4} \overset{•}{2}$ 写成分数的形式是．

查看试题解析

三、解答题

17. 计算：

(1)、 $4 - (- 5) - 6 + (- 2)$

(2)、 $8 \div {(- 2)}^{2} - (- 4) \times (- 3)$

查看试题解析
18. 如图，已知点A、B、C ，根据下列语句画图：（尺规作图，要保留作图痕迹．）

⑴画出直线AB；

⑵画出射线AC；

⑶在线段AB的延长线上截取线段BD ，使得AD=AB+BC；

⑷画出线段CD ．

查看试题解析
19. 解下列方程：

(1)、2x-7=x-3；

(2)、 $\frac{x + 1}{2} = \frac{2 - x}{3} + 1$

查看试题解析
20. 探索规律：
观察下面由※组成的图案和算式，填空（直接写出答案）：

$\begin{array}{l} 1 + 3 = 4 = 2^{2} \\ 1 + 3 + 5 = 9 = 3^{2} \\ 1 + 3 + 5 + 7 = 16 = 4^{2} \\ 1 + 3 + 5 + 7 + 9 = 25 = 5^{2} \end{array}$

⑴请猜想1+3+5+7+9+11=；

⑵请猜想1+3+5+7+9+……+（2n-1）=；

⑶请用上述规律计算：41+43+45+……+97+99= ．

查看试题解析
21. 古代名著《算学启蒙》中有一题：良马日行二百四十里，驽马日行一百五十里，驽马先行十二日，问良马几何追及之．意思是：跑得快的马每天走240里，跑得慢的马每天走150里，慢马先走12天，问快马几天可追上慢马，请你用方程的知识解答上述问题．

查看试题解析
22. 如图，已知∠AOB=140 $°$ ，∠COE与∠EOD互余，OE平分∠AOD．

(1)、若∠COE=38 $°$ ，求∠DOE和∠BOD的度数；

(2)、设∠COE=α，∠BOD=β，请探究α与β之间的数量关系．

查看试题解析
23. 定义如下：使等式 $a b = a^{2} - 2 b - 2$ 成立的一对有理数a，b叫“理想有理数对”，记为（a，b），如： $4 \times \frac{7}{3} = 4^{2} - 2 \times \frac{7}{3} - 2$ ，所以数对（4， $\frac{7}{3}$ ）是“理想有理数对”．

(1)、判断数对（-1，1）是否为“理想有理数对”，并说明理由；

(2)、若数对（-3，m）是“理想有理数对”，求m的值，并求代数式 $m^{2} - 3 (1 - m)$ 的值．

查看试题解析

24. 一种商品按销售量分三部分制定销售单价，如下表：

销售量	单价
不超过100件的部分	2.8元/件
超过100件不超过300件的部分	2.2元/件
超过300件的部分	2元/件

(1)、若买100件花元，买300件花元；买380件花元；

(2)、小明买这种商品花了500元，求购买了这种商品多少件；

(3)、若小明花了n元（n>280），恰好购买0.4n件这种商品，求n的值．

查看试题解析

25. （背景知识）数轴上A、B两点在数轴上对应的数为a、b，则A、B两点之间的距离定义为：AB=|b-a|．
（问题情境）已知点A、B、O在数轴上表示的数分别为-6、10和0，点M、N分别从O、B出发，同时向左匀速运动，点M的速度是每秒1个单位长度，点N的速度是每秒3个单位长度，设运动的时间为t秒（t>0)，

(1)、填空：①OA= ． OB=；
②用含t的式子表示：AM=；AN=；

(2)、当t为何值时，恰好有AN=2AM；

(3)、求|t-6|+|t+10|的最小值．

查看试题解析