山西省阳泉市平定县2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 中国是世界上最早认识和应用负数的国家，比西方早一千多年，在我国古代著名的数学专著《九章算术》中，首次引入负数，如果收入100元记作+100元，则﹣60元表示（）

A、支出40元 B、收入40元 C、支出60元 D、收入60元

查看试题解析
2. 下列判断中错误的是（）

A、﹣3的相反数为3 B、5的倒数是 $- \frac{1}{5}$ C、﹣8是负整数 D、﹣4，﹣1，0中最小的数是﹣4

查看试题解析
3. 母亲节这天，小明和妈妈到花店买花，每枝玫瑰是10元，每枝康乃馨是6元，小明买了a枝玫瑰，b枝康乃馨共花（）

A、16a元 B、16b元 C、16（a+b）元 D、（10a+6b）元

查看试题解析
4. 圆锥侧面展开图可能是下列图中的（）

A、 B、 C、 D、

查看试题解析
5. 第二届中国国际进口博览会于2019年11月5日至10日在上海举办，共有181个国家、地区和国际组织参会，3800多家企业参加企业展，约500000名境内外专业采购商到会洽谈采购．将500000用科学记数法表示为（）

A、500000×10⁵ B、5×10⁶ C、5×10⁵ D、0.5×10⁶

查看试题解析
6. 数轴是数形结合思想的产物．有了数轴以后，可以用数轴上的点直观地表示有理数，这样就建立起了“数”与“形”之间的联系．同时，数轴也是我们研究相反数、绝对值的直观工具．如图，数轴上有A，B，C，D四个点，其中所对应的数的绝对值最小的点是（）

A、点A B、点B C、点C D、点D

查看试题解析
7. 下列变形中，正确的是（）

A、若5x﹣6＝7，则5x＝7﹣6 B、若 $5 b^{2} - 3 c^{2} - (3 b^{2} - 3 c^{2}) + c^{2} + 2016 a b c$ ，则2（x﹣1）+3（x+1）＝1 C、若﹣3x＝5，则x＝﹣ $\frac{3}{5}$ D、若5x﹣3＝4x+2，则5x﹣4x＝2+3

查看试题解析
8. 某校在庆祝祖国70周年“我和我的祖国”中学生读书系列活动中，将一些科技类图书分给了七年级一班的学生阅读，如果每人分4本，则剩余20本；如果每人分5本，则还缺30本．若设该校七年级一班有学生x人，则下列方程正确的是（）

A、4x﹣20＝5x+30 B、4x+20＝5x﹣30 C、4x﹣20＝5x﹣30 D、4x+20＝5x+30

查看试题解析
9. 如图，直线AB、CD相交于点O，射线OM平分 $∠ AOC$ ， $∠ MON = 90^{\circ} .$ 若 $∠ MOC = 35^{\circ}$ ，则 $∠ BON$ 的度数为 $($ $)$

A、 $35^{\circ}$ B、 $45^{\circ}$ C、 $55^{\circ}$ D、 $64^{\circ}$

查看试题解析
10. 如图，用黑白两色正方形瓷砖按一定规律铺设地板图案，第101个图案中白色瓷砖块数是（）

A、305 B、302 C、296 D、204

查看试题解析

二、填空题

11. 写出 $- \frac{2}{3} x^{3} y^{4}$ 的一个同类项：．

查看试题解析
12. 如图，在利用量角器画一个40°的∠AOB的过程中，对于先找点B，再画射线OB这一步骤的画图依据，喜羊羊同学认为是两点确定一条直线，懒羊羊同学认为是两点之间线段最短．你认为同学的说法是正确的．

查看试题解析
13. 为了进一步推进“不忘初心，牢记使命”主题教育活动，某单位组织34人分别到红育口爱国主义教育基地和七亘大捷纪念馆进行了主题党日系列活动，到红育口爱国主义教育基地的人数比到七亘大捷纪念馆的人数的2倍多1人，求到两地的人数各是多少．设到七亘大捷纪念馆的人数为x人，请列出满足题意的一元一次方程．

查看试题解析
14. 如图，将边长为3a的正方形沿虚线剪成两块正方形和两块长方形，若拿掉边长为2b的小正方形后，再将剩下的三块拼成一块矩形，则这块矩形较长的边长为．

查看试题解析
15. 如图，点C为线段AB上一点，点C将AB分成2：3两部分，M是AC的中点，N是BC的中点，若AN＝35cm，则AB的长为cm．

查看试题解析

三、解答题

16.

(1)、计算：（﹣16）﹣5+（﹣14）﹣（﹣26）；

(2)、计算：﹣4²÷（﹣4）²+5×（﹣6）+3³+|﹣8|．

查看试题解析
17. 解方程： $\frac{x - 1}{3}$ ＝1﹣ $\frac{2 x - 3}{2}$ ．

查看试题解析
18. 化简求值：2（x²y﹣xy²﹣1）﹣3（2x²y﹣3xy²﹣3），其中x＝﹣ $\frac{1}{2}$ ，y＝1．

查看试题解析
19. 在班级元旦联欢会上，主持人邀李强、张华两位向学参加一个游戏．游戏规则是每人每次抽取四张卡片．如果抽到白色卡片，那么加上卡片上的数字；如果抽到黑色卡片，那么减去卡片上的数字，比较两人所抽4张卡片的计算结果，结果较小的为同学们唱歌，李强同学抽到如图（1）所示的四张卡片，张华同学抽到如图（2）所示的四张卡片．李强、张华谁会为同学们唱歌？

查看试题解析
20. 某公园准备修建一块长方形草坪，长为a米，宽为b米.并在草坪上修建如图所示的十字路，已知十字路宽2米.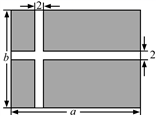

(1)、用含a、b的代数式表示修建的十字路的面积.

(2)、若a=30，b=20，求草坪（阴影部分）的面积.

查看试题解析
21. 阅读并解答问题：
数学大师的名题与方程

欧拉是18世纪瑞士著名的数学大师．他的一生都致力于数学各个领域的研究，并取得非凡的成就．在他所著的《代数学入门》一书中就曾经出现过好几道和遗产分配有关的数学问题．他构思这些问题的初衷，正是为了强化方程解题的适用和便利．

请用适当的方法解答下面问题：

父亲死后，四个儿子按下述方式分了他的财产：老大拿了财产的一半少3000英镑：老二拿了财产的 $\frac{1}{3}$ 少1000英镑；老三拿了恰好是财产的 $\frac{1}{4}$ ；老四拿了财产的 $\frac{1}{5}$ 加上600英镑．问整个财产有多少？每个儿子各分了多少？

查看试题解析
22. 为庆祝国庆节，某市中小学统一组织文艺汇演，甲、乙两所学校共92人（其中甲校人数多于乙校人数，且甲校人数不够90人）准备统一购买服装参加演出，下面是某服装厂给出的演出服装的价格表：

购买服装的套数

1套至45套

46套至90套

91套及以上

每套服装的价格

60元

50元

40元

如果两所学校分别单独购买服装，一共应付5000元．

(1)、甲、乙两所学校各有多少学生准备参加演出？

(2)、如果甲、乙两所学校联合起来购买服装，那么比各自购买服装共可以节省多少钱？

查看试题解析
23. 综合与探究
（实践操作）三角尺中的数学

数学实践活动课上，“奋进”小组将一副直角三角尺的直角顶点叠放在一起，如图1，使直角顶点重合于点C．

(1)、（问题发现）
①填空：如图1，若∠ACB＝145°，则∠ACE的度数是， ∠DCB的度数， ∠ECD的度数是．

②如图1，你发现∠ACE与∠DCB的大小有何关系？；∠ACB与∠ECD的大小又有何关系？。

(2)、（类比探究）
如图2，当△ACD与△BCE没有重合部分时，上述②中你发现的结论是否还依然成立？请说明理由．

查看试题解析

购买服装的套数	1套至45套	46套至90套	91套及以上
每套服装的价格	60元	50元	40元