内蒙古通辽市科尔沁区2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-11-16 类型:期末考试
一、单选题
-
1. 一5的绝对值是( )A、5 B、 C、 D、-52. 如图所示,下列表示 的方法中,正确的是( )
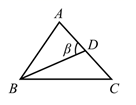 A、 B、 C、 D、3. 如图所示,则下列判断正确的是( )
A、 B、 C、 D、3. 如图所示,则下列判断正确的是( ) A、 B、 C、 D、4. 我国作家莫言获得诺贝尔文学之后,他的代表作品《蛙》的销售量就比获奖之前增长了180倍,达到5100000册.把5100000用科学记数法表示为( )A、 B、 C、 D、5. 如图,下列条件不能说明 平分 的是( )
A、 B、 C、 D、4. 我国作家莫言获得诺贝尔文学之后,他的代表作品《蛙》的销售量就比获奖之前增长了180倍,达到5100000册.把5100000用科学记数法表示为( )A、 B、 C、 D、5. 如图,下列条件不能说明 平分 的是( )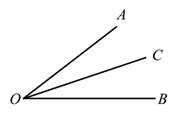 A、 B、 C、 D、6. 下列运算中,正确的是( )A、 B、 C、 D、7. 如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
A、 B、 C、 D、6. 下列运算中,正确的是( )A、 B、 C、 D、7. 如图是一个正方体纸盒的外表面展开图,则这个正方体是( )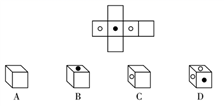 A、A B、B C、C D、D8. 下列变形错误的是( )A、如果 ,则 B、如果 ,则 C、如果 ,则 D、如果 ,则9. 一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图,搜救船位于图中圆心 处,事故船位于距 点40海里的 处,雷达操作员要用方位角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式正确的为( )
A、A B、B C、C D、D8. 下列变形错误的是( )A、如果 ,则 B、如果 ,则 C、如果 ,则 D、如果 ,则9. 一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图,搜救船位于图中圆心 处,事故船位于距 点40海里的 处,雷达操作员要用方位角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式正确的为( ) A、事故船在搜救船的北偏东 方向 B、事故船在搜救船的北偏东 方向 C、事故船在搜救船的南偏西 方向 D、事故船在搜救船的南偏西 方向10. 甲船从 地开往 地,航速为35千米/时,乙船由 地开往 地,航速为25千米/时,甲船先航行2小时后,乙船再出发,两船在距 地120千米处相遇,求两地的距离.若设两地的距离为 千米,根据题意可列方程为( )A、 B、 C、 D、
A、事故船在搜救船的北偏东 方向 B、事故船在搜救船的北偏东 方向 C、事故船在搜救船的南偏西 方向 D、事故船在搜救船的南偏西 方向10. 甲船从 地开往 地,航速为35千米/时,乙船由 地开往 地,航速为25千米/时,甲船先航行2小时后,乙船再出发,两船在距 地120千米处相遇,求两地的距离.若设两地的距离为 千米,根据题意可列方程为( )A、 B、 C、 D、二、填空题
-
11. 某种零件,标明要求是φ20±0.2 mm(φ表示直径,单位:毫米),经检查,一个零件的直径是19.9mm,该零件(填“合格” 或“不合格”).12. 若 和 是同类项,则 =.13. 几何并不复杂,生活中处处有几何.修高速的时候,通过修建高架桥和隧道,把地形复杂的两点之间的公路修成直道,用到的几何原理是 .14. °.15. 已知 , 在同一直线上,则 .16. 已知 ,则代数式 的值为 .17. 一家商店某种裤子按成本价提高 后标价,又以八折优惠卖出,结果每条裤子获利10元,则这条裤子的成本是 .
三、解答题
-
18. 计算:(1)、(2)、19. 解下列方程:(1)、 ;(2)、20. 一个角的补角比这个角的余角3倍还多 ,求这个角的度数.21. 先化简,再求值: ,其中 .22. 如图,点 是线段 上一点,且 .
 (1)、求线段 的长;(2)、如果 是线段 的中点, 是线段 的中点,求线段 的长.23. 《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少.请解答上述问题.24. 一出租车某一天以家为出发地在东西两方向营运,向东为正,向西为负,行车里程(单位: )依先后次序记录如下: .(1)、将最后一个乘客送到目的地时,出租车离家多远?在家什么方向?(2)、若每千米的价格为2元,则司机一天的营业额是多少?(3)、如果出租车送走最后一名乘客后需要返回家中,且出租车每千米耗油 升,每升汽油6元,不计汽车的损耗,那么出租车司机收工回家是盈利还是亏损了?盈利(或亏损)多少钱?25. 在“节能减排,做环保小卫士”的活动中,小王对两种照明灯的使用情况进行了调查,得出如下表所示的数据:
(1)、求线段 的长;(2)、如果 是线段 的中点, 是线段 的中点,求线段 的长.23. 《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少.请解答上述问题.24. 一出租车某一天以家为出发地在东西两方向营运,向东为正,向西为负,行车里程(单位: )依先后次序记录如下: .(1)、将最后一个乘客送到目的地时,出租车离家多远?在家什么方向?(2)、若每千米的价格为2元,则司机一天的营业额是多少?(3)、如果出租车送走最后一名乘客后需要返回家中,且出租车每千米耗油 升,每升汽油6元,不计汽车的损耗,那么出租车司机收工回家是盈利还是亏损了?盈利(或亏损)多少钱?25. 在“节能减排,做环保小卫士”的活动中,小王对两种照明灯的使用情况进行了调查,得出如下表所示的数据:耗电量
使用寿命
价格
一盏普通灯
度/时
2000小时
3元/盏
一盏节能灯
度/时
4000小时
31元/盏
已知这两种灯的照明效果一样,电价为每度 元. (注:费用=灯的售价+电费)
请你解决以下问题:
(1)、在普通灯的使用寿命内,设照明时间为 小时,请用含x的式子分别表示用一盏普通灯的费用和用一盏节能灯的费用;(2)、在普通灯的使用寿命内,照明多少小时,使用这两种灯的费用相等?(3)、如果计划照明4000小时,购买哪一种灯更省钱?请你通过计算说明理由.26. 问题情境:以直线 上一点 为端点作射线 ,将一个直角三角形的直角顶点放在 处( ).(1)、如图1,直角三角板 的边 放在射线 上, 平分 和 重合,则 ;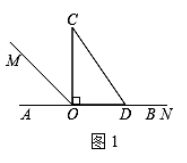 (2)、直角三角板 绕点 旋转到如图2的位置, 平分 平分 ,求 的度数.
(2)、直角三角板 绕点 旋转到如图2的位置, 平分 平分 ,求 的度数. (3)、直角三角板 绕点 旋转到如图3的位置, 平分 平分 ,猜想 的度数,并说明理由.
(3)、直角三角板 绕点 旋转到如图3的位置, 平分 平分 ,猜想 的度数,并说明理由.