山西省运城市芮城县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-13 类型:期末考试
一、单选题
-
1. 下列各组数中,属于勾股数的是( )A、1, ,2 B、1.5,2,2.5 C、6,8,10 D、5,6,72. 在下列各数: 、0.2、-π、 、 、 中无理数的个数是( )A、1 B、2 C、3 D、43. 在解二元一次方程组时,我们的基本思路是“消元”,即通过“代入法”或“加减法”将“二元”化为“一元”,这个过程体现的数学思想是( )A、数形结合思想 B、转化思想 C、分类讨论思想 D、类比思想4. 已知 是二元一次方程组 的解,那么 x+y 的值是( )
A、0 B、5 C、-1 D、15. 已知直线m∥n,将一块含45°角的直角三角板ABC按如图方式放置,其中斜边BC与直线n交于点D.若∠1=25°,则∠2的度数为( )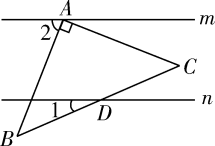 A、60° B、65° C、70° D、75°6. 在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的( )A、平均数 B、中位数 C、众数 D、方差7. 已知函数y=kx+b的图象如图所示,则函数y=-bx+k的图象大致是( )
A、60° B、65° C、70° D、75°6. 在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的( )A、平均数 B、中位数 C、众数 D、方差7. 已知函数y=kx+b的图象如图所示,则函数y=-bx+k的图象大致是( )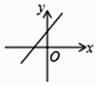 A、
A、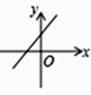 B、
B、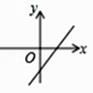 C、
C、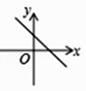 D、
D、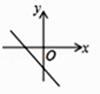 8. 《九章算术》是中国古代第一部数学专著,它对我国古代后世的数学家产生了深远的影响,该书中记载了一个问题,大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价几何?设有x人,物品价值y元,则所列方程组正确的是( )A、 B、 C、 D、9. 下列命题①同位角相等;②相等的角是对顶角;③同角或等角的补角相等;④三角形的一个外角大于任何一个内角.其中是真命题有( )A、0个 B、1个 C、2个 D、3个10. 如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )
8. 《九章算术》是中国古代第一部数学专著,它对我国古代后世的数学家产生了深远的影响,该书中记载了一个问题,大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价几何?设有x人,物品价值y元,则所列方程组正确的是( )A、 B、 C、 D、9. 下列命题①同位角相等;②相等的角是对顶角;③同角或等角的补角相等;④三角形的一个外角大于任何一个内角.其中是真命题有( )A、0个 B、1个 C、2个 D、3个10. 如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( ) A、∠A+∠C+∠D+∠E=360° B、∠A-∠C+∠D+∠E=180° C、∠E-∠C+∠D-∠A=90° D、∠A+∠D=∠C+∠E
A、∠A+∠C+∠D+∠E=360° B、∠A-∠C+∠D+∠E=180° C、∠E-∠C+∠D-∠A=90° D、∠A+∠D=∠C+∠E二、填空题
-
11. 有一个数值转换器,原理如下:当输入的x为64时,输出的y是.
 12. 学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛,在选拔过程中,每人射击10次,计算他们的平均成绩及方差如下表:
12. 学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛,在选拔过程中,每人射击10次,计算他们的平均成绩及方差如下表:选手
甲
乙
平均数(环)
9.5
9.5
方差
0.035
0.015
请你根据上表中的数据选一人参加比赛,最适合的人选是 .
13. 规定用符号[m]表示一个实数m的整数部分,例如:[]=0,[3.14]=3.按此规定[+1]的值为14. 如图,在△ABC中,点D、E分别在边AB、AC上,如果∠A=40°,那么∠1+∠2的大小为. 15. 如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 .
15. 如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 .
三、解答题
-
16.(1)、计算:(2)、解方程组:17. 如图, 在正方形网格中,每个小正方形的边长均为1,若点A的坐标为 ,按要求回答下列问题:
 (1)、在图中建立适当的平面直角坐标系,并写出点B和点C的坐标;(2)、作出 关于x轴对称的图形 .(不用写作法)18. 某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果期末评价成绩80分以上(含80分),则评为“优秀”.下面表中是小张和小王两位同学的成绩记录:
(1)、在图中建立适当的平面直角坐标系,并写出点B和点C的坐标;(2)、作出 关于x轴对称的图形 .(不用写作法)18. 某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果期末评价成绩80分以上(含80分),则评为“优秀”.下面表中是小张和小王两位同学的成绩记录:完成作业
单元测试
期末考试
小张
70
90
80
小王
60
75
(1)、若按三项成绩的平均分记为期末评价成绩,请计算小张的期末评价成绩;(2)、若按完成作业、单元检测、期末考试三项成绩按 的权重来确定期末评价成绩.①请计算小张的期末评价成绩为多少分?
②小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?
19. 2020年是全面建成小康社会收官之年,某扶贫帮扶小组积极响应,对农民实施精准扶贫.某农户老张家种植花椒和黑木耳两种干货共800千克,扶贫小组通过市场调研发现,花椒市场价60元/千克,黑木耳市场价48元/千克,老张全部售完可以收入4.2万元.已知老张种植花椒成本需25元/千克,种植木耳成本需35元/千克,根据脱贫目标任务要求,老张种植花椒和黑木耳的两种干货的纯收入(销售收入-种植成本)在2万元以上才可以顺利脱贫.请你分析一下扶贫帮扶小组是否能帮助老张顺利脱贫.20. 某通讯公司推出①,②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分)与费用y(元)之间的函数关系如图所示. (1)、有月租的收费方式是(填“①”或“②”),月租费是元;(2)、分别求出①,②两种收费方式中y与自变量x之间的函数表达式;(3)、请你根据用户通讯时间的多少,给出经济实惠的选择建议.21. 如图,已知四边形ABCD中,∠D=∠B=90°,AE平分∠DAB,CF平分∠DCB.试判断∠AEF与∠CFE是否相等?并证明你的结论.
(1)、有月租的收费方式是(填“①”或“②”),月租费是元;(2)、分别求出①,②两种收费方式中y与自变量x之间的函数表达式;(3)、请你根据用户通讯时间的多少,给出经济实惠的选择建议.21. 如图,已知四边形ABCD中,∠D=∠B=90°,AE平分∠DAB,CF平分∠DCB.试判断∠AEF与∠CFE是否相等?并证明你的结论. 22. 综合与探究:
22. 综合与探究:将三角形纸板如图放置,点P是边AB边上一点,DF∥CE,∠PCE=∠α,∠PDF=∠β,
探究:
 (1)、如果α=30°,β=40°,则∠DPC=.(2)、当点P在E、F两点之间运动时,∠DPC与α、β之间有何数量关系?并说明理由;
(1)、如果α=30°,β=40°,则∠DPC=.(2)、当点P在E、F两点之间运动时,∠DPC与α、β之间有何数量关系?并说明理由;拓展:
(3)、猜想:如果点P在E、F两点外侧运动时(点P与点A、B、E、F四点不重合),上述(2)中的结论是否还成立?并说明理由.
23. 综合与实践如图,直线 的函数关系式为 ,且 与 轴交于点A , 直线 经过点B(2,0),C(-1,3),直线 与 交于点D .
 (1)、求直线 的函数关系式;(2)、求△ABD的面积.(3)、点P是 轴上一动点,问是否存在一点P,恰好使△ADP为直角三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(1)、求直线 的函数关系式;(2)、求△ABD的面积.(3)、点P是 轴上一动点,问是否存在一点P,恰好使△ADP为直角三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.