山西省忻州市2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-13 类型:期末考试
一、单选题
-
1. 计算 的结果是( )A、1 B、-1 C、3 D、-32. 若分式 的值为0,则 的值为( )A、0 B、1 C、-2 D、3. 如图,在 中, , , 是 的角平分线,则 的度数为( )
 A、 B、 C、 D、4. 如图,将△ABC的三个顶点坐标的横坐标都乘以-1,并保持纵坐标不交,则所得图形与原图形的关系是( )
A、 B、 C、 D、4. 如图,将△ABC的三个顶点坐标的横坐标都乘以-1,并保持纵坐标不交,则所得图形与原图形的关系是( )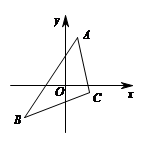 A、关于x轴对称 B、关于y轴对称 C、将原图形沿x轴的负方向平移了1个单位 D、将原图形沿y轴的负方向平移了1个单位5. 计算 的结果是( )A、 B、 C、 D、6. 分式方程 的解为( )A、 B、 C、 D、7. 下列因式分解正确的是( )A、 B、 C、 D、8. 若 ,则 的值是( )A、 B、 C、 D、9. 某单位购进一种垃圾分类机器人,据实验分析:在对生活垃圾进行分类时,机器人分类120桶所用的时间与人工分类90桶所用的时间相同,已知机器人每小时比人工多分类20桶垃圾.若设机器人每小时分类 桶垃圾,则可列方程为( )
A、关于x轴对称 B、关于y轴对称 C、将原图形沿x轴的负方向平移了1个单位 D、将原图形沿y轴的负方向平移了1个单位5. 计算 的结果是( )A、 B、 C、 D、6. 分式方程 的解为( )A、 B、 C、 D、7. 下列因式分解正确的是( )A、 B、 C、 D、8. 若 ,则 的值是( )A、 B、 C、 D、9. 某单位购进一种垃圾分类机器人,据实验分析:在对生活垃圾进行分类时,机器人分类120桶所用的时间与人工分类90桶所用的时间相同,已知机器人每小时比人工多分类20桶垃圾.若设机器人每小时分类 桶垃圾,则可列方程为( ) A、 B、 C、 D、10. 如图,已知 且 ,连接 ,分别过点 作 , ,垂足分别为 .若 , , ,则 的长为( )
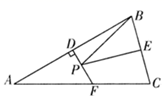
A、 B、 C、 D、10. 如图,已知 且 ,连接 ,分别过点 作 , ,垂足分别为 .若 , , ,则 的长为( )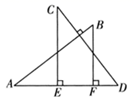 A、4 B、 C、3 D、
A、4 B、 C、3 D、二、解答题
-
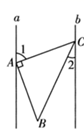
11. 若 ,则代数式 的值为 .12. 2019年华为发布 “鲲鹏920”计算芯片:64核心业内性能最强! 也就是0.000000007 ,数据0.000000007 可以用科学记数法表示为m.13. 如图, ,点 在直线a上,点 在直线b上, , ,若 ,则 的度数为 .
 14. 如图,已知 和 相交于点 且 ,分别连接 ,已知 , ,则 的度数为°.
14. 如图,已知 和 相交于点 且 ,分别连接 ,已知 , ,则 的度数为°.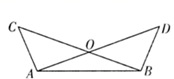 15.(1)、因式分解:(2)、计算:16. 先化简,再求值: ,其中 .17. 如图所示,在 的正方形网格中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”. 是一个格点三角形,请你在图1,图2,图3中分别画出一个与 成轴对称的格点三角形,并将所画三角形涂上阴影.(注:所画的三个图不能重复.)
15.(1)、因式分解:(2)、计算:16. 先化简,再求值: ,其中 .17. 如图所示,在 的正方形网格中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”. 是一个格点三角形,请你在图1,图2,图3中分别画出一个与 成轴对称的格点三角形,并将所画三角形涂上阴影.(注:所画的三个图不能重复.)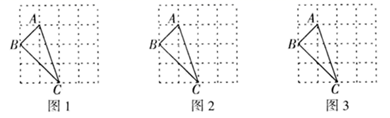 18. 如图,在 中, .
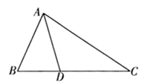
18. 如图,在 中, .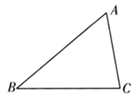 (1)、利用尺规作 的平分线 ,交 于点 ,并在图中标明相应字母.(保留作图痕迹,不写作法)(2)、延长 到点 (不要求尺规作图),使 ,猜想线段 与 的关系,并说明理由.19. 观察下列两位数(十位数字相同,个位数字的和是10)相乘的等式.
(1)、利用尺规作 的平分线 ,交 于点 ,并在图中标明相应字母.(保留作图痕迹,不写作法)(2)、延长 到点 (不要求尺规作图),使 ,猜想线段 与 的关系,并说明理由.19. 观察下列两位数(十位数字相同,个位数字的和是10)相乘的等式.; ; ; ; ;…
我们发现了一个速算法则:两个两位数相乘,如果这两个乘数的十位数字相同,个位数字的和是10,该类乘法的速算方法是:将其中一个乘数的十位数字与另一个乘数的十位数字加1的和相乘,所得的积作为计算结果的前两位(即千位和百位,数位不足两位的,千位看作0);再将两个乘数的个位数字相乘,所得的积作为计算结果的后两位是 ,它们乘积的后两位是 ,所以 .请解答下列问题:
(1)、计算: ;(2)、若设其中一个乘数的十位数字为 ,个位数字是 ( 表示1到9的整数).请通过计算解释速算法则.20. 某商场用9000元购进一批新款保暖内衣,上架后很快销售一空,商场又紧急购进第二批,数量是第一批的2倍,但每件的进价涨了10元,第二批共用去21000元.求该商场第一批购进这种保暖内衣多少件?21. 阅读理解,并解决问题.分式方程的增根:解分式方程时可能会产生增根,原因是什么呢?事实上,解分式方程时产生增根,主要是在去分母这一步造成的.根据等式的基本性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.但是,当等式两边同乘0时,就会出现 的特殊情况.因此,解方程时,方程左右两边不能同乘0.而去分母时会在方程左右两边同乘公分母,此时无法知道所乘的公分母的值是否为0,于是,未知数的取值范围可能就扩大了.如果去分母后得到的整式方程的根使所乘的公分母值为0,此根即为增根,增根是整式方程的根,但不是原分式方程的根.所以解分式方程必须验根.请根据阅读材料解决问题:
(1)、若解分式方程 时产生了增根,这个增根是;(2)、小明认为解分式方程 时,不会产生增根,请你直接写出原因;(3)、解方程22. 已知,在等边三角形 中, 为 边上的高.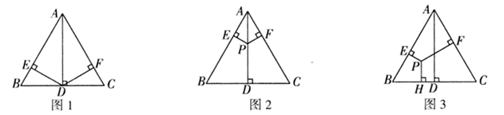 (1)、操作发现:如图1,过点 分别作 , ,垂足分别为 .请直接写出 和 的数量关系;(2)、如图2,若点 为 上任意一点(不与 重合),过点 作 , ,垂足分别为 .判断 和 的数量关系,并说明理由;(3)、拓广探索:
(1)、操作发现:如图1,过点 分别作 , ,垂足分别为 .请直接写出 和 的数量关系;(2)、如图2,若点 为 上任意一点(不与 重合),过点 作 , ,垂足分别为 .判断 和 的数量关系,并说明理由;(3)、拓广探索:如图3,点 为等边三角形 内任意一点,过点 作 , , ,垂足分别为 ,探究 和 的数量关系,并说明理由.
三、填空题
-
23. 如图,在 中, , , ,点 分别是 的中点,点 在 上,且 .若点 为线段 上一动点,连接 ,则 周长的最小值是 .