山西省吕梁市孝义市2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-13 类型:期末考试
一、单选题
-
1. 下列长度的三条线段能组成三角形的是( )A、8,4,3 B、5,6,11 C、3,4,5 D、4,5,102. 将一副三角板按图中方式叠放,则 的度数为( )
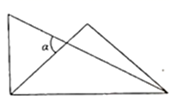 A、 B、 C、 D、3. 如图,已知 ,添加下列条件不能判定 的是( )
A、 B、 C、 D、3. 如图,已知 ,添加下列条件不能判定 的是( ) A、 B、 C、 D、4. 点P(-2,3)关于y轴的对称点的坐标是( )A、(2,3) B、(-2,3) C、(2,-3) D、(-2,-3)5. 下列汽车标志中,不是轴对称图形的是( )A、
A、 B、 C、 D、4. 点P(-2,3)关于y轴的对称点的坐标是( )A、(2,3) B、(-2,3) C、(2,-3) D、(-2,-3)5. 下列汽车标志中,不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列运算正确的是( )A、 B、 C、 D、7. 下列各式错误的是( )A、 B、 C、 D、8. 一艘轮船在静止中的最大航速为 ,它以最大航速沿江顺流航行 所用时间,与以最大航速逆流航行 所用时间相等,江水的流速为多少?设江水流速为 ,则下列方程正确的是( )A、 B、 C、 D、9. 如图,等腰 中 , 垂直平分 ,交 于点 ,交 于点 ,点 是线段 上的一动点,若 的面积是 , ,则 的周长最小值是( )
6. 下列运算正确的是( )A、 B、 C、 D、7. 下列各式错误的是( )A、 B、 C、 D、8. 一艘轮船在静止中的最大航速为 ,它以最大航速沿江顺流航行 所用时间,与以最大航速逆流航行 所用时间相等,江水的流速为多少?设江水流速为 ,则下列方程正确的是( )A、 B、 C、 D、9. 如图,等腰 中 , 垂直平分 ,交 于点 ,交 于点 ,点 是线段 上的一动点,若 的面积是 , ,则 的周长最小值是( ) A、 B、 C、 D、10. 如图,在 中, 是 上一点, , 是 上一点, ,下列一定正确的是( )
A、 B、 C、 D、10. 如图,在 中, 是 上一点, , 是 上一点, ,下列一定正确的是( )
① ;② ;③ .
A、①② B、①③ C、②③ D、①②③二、填空题
-
11. 因式分解:12. 细胞是生物体的机构和功能单位. 人体细胞约40万亿—60万亿个,细胞的平均直径在10—20微米之间(1微米=0. 000001米),用科学记数法表示20微米=米.13. 庆祝中华人民共和国成立70周年大阅兵于2019年10月10日在北京天安门广场举行. 通常提到的“阅兵”实际分为“阅兵式”和“分列式”. 阅兵式就是士兵不动,军委主席检阅,分列式就是所有方(梯)队,踏着整齐的节奏,依次通过天安门前检阅区,这也是最振奋人心的时刻,在分列式中,受检阅的距离就是天安门前东西两个华表之间,已知两个华表之间的距离是96米,通过这段距离需要68秒,步速每分钟 步,请用含 的式子表示每步的长度为米.
 14. 如图,已知 ,则
14. 如图,已知 ,则 15. 如图,已知 中, ,则
15. 如图,已知 中, ,则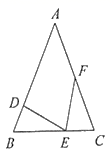
三、解答题
-
16.(1)、计算:(2)、(3)、先化简 ,再从 中选一个你认为合适的数 代入求值.17. 解方程: .18. 已知:如图, , 、 分别是 、 的对应边上的高.求证: .
 19. 作图题:如图,已知 ,线段 ,求作 ,使 . (尺规作图,不写作法,保留作图痕迹).
19. 作图题:如图,已知 ,线段 ,求作 ,使 . (尺规作图,不写作法,保留作图痕迹).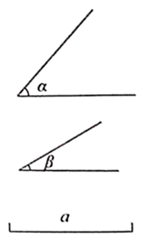 20. 阅读下列材料,并完成任务. 三角形的外心定义:三角形三边的垂直平分线相交于一点,这个点叫做三角形的外心,如图1,直线 分别是边 的垂直平分线.
20. 阅读下列材料,并完成任务. 三角形的外心定义:三角形三边的垂直平分线相交于一点,这个点叫做三角形的外心,如图1,直线 分别是边 的垂直平分线.
求证:直线 相交于一点.
证明:如图2,设 相交于点 ,分别连接
∵ 是 的垂直平分线,
∴ ,(依据1)
∵ 是 的垂直平分线,
∴ ,
∴ ,(依据2)
∵ 是 的垂直平分线,
∴点 在 上,(依据3)
∴直线 相交于一点.
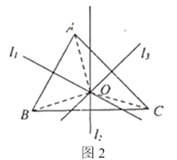
 (1)、上述证明过程中的“依据1”“依据2”“依据3”分别指什么?(2)、如图3,直线 分别是 的垂直平分线,直线 相交于点 ,点 是 的外心, 交 于点 , 交 于点 ,分别连接 、 、 、 、 .若 , 的周长为 ,求 的周长.21. 随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,同时也给自行车商家带来商机. 某自行车行销售 型, 型两种自行车,经统计,2019年此车行销售这两种自行车情况如下: 自行车销售总额为8万元. 每辆 型自行车的售价比每辆 型自行车的售价少200元, 型自行车销售数量是 自行车的1. 25倍, 自行车销售总额比A型自行车销售总额多 .(1)、求每辆 型自行车的售价多少元.(2)、若每辆 型自行车进价1400元,每辆 型自行车进价1300元,求此自行车行2019年销售 型自行车的总利润.22. 如图, 中, ,已知 , 与 相交于点 , 与 相交于点 , 与 相交于点 .
(1)、上述证明过程中的“依据1”“依据2”“依据3”分别指什么?(2)、如图3,直线 分别是 的垂直平分线,直线 相交于点 ,点 是 的外心, 交 于点 , 交 于点 ,分别连接 、 、 、 、 .若 , 的周长为 ,求 的周长.21. 随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,同时也给自行车商家带来商机. 某自行车行销售 型, 型两种自行车,经统计,2019年此车行销售这两种自行车情况如下: 自行车销售总额为8万元. 每辆 型自行车的售价比每辆 型自行车的售价少200元, 型自行车销售数量是 自行车的1. 25倍, 自行车销售总额比A型自行车销售总额多 .(1)、求每辆 型自行车的售价多少元.(2)、若每辆 型自行车进价1400元,每辆 型自行车进价1300元,求此自行车行2019年销售 型自行车的总利润.22. 如图, 中, ,已知 , 与 相交于点 , 与 相交于点 , 与 相交于点 .
 (1)、如图,观察并猜想 和 有怎样的数量关系?并说明理由.(2)、筝形的定义:两组邻边分别相等的四边形叫做筝形. 如上图,证明四边形 是筝形.(3)、如图,若 ,其他条件不变,求 的长度.
(1)、如图,观察并猜想 和 有怎样的数量关系?并说明理由.(2)、筝形的定义:两组邻边分别相等的四边形叫做筝形. 如上图,证明四边形 是筝形.(3)、如图,若 ,其他条件不变,求 的长度.