山西省吕梁市文水县2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-13 类型：期末考试

进入出卷网下载

一、单选题

1. 分式 $\frac{1}{x + 2}$ 在实数范围内有意义,则实数 $x$ 的取值范围是（）

A、 $x > 2$ B、 $x > - 2$ C、 $x \neq - 2$ D、 $x < - 2$

查看试题解析
2. 窗花是贴在窗纸或窗户玻璃上的剪纸，是中国古老的民间艺术之一.窗花的内容丰富、题材广泛，以其特有的概括和夸张手法将吉事祥物、美好愿望表现得淋漓尽致.下列窗花的图案中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 以下列各组线段为边，能组成三角形的是（）

A、2，3，5 B、3，3，7 C、8，6，3 D、6，7，14

查看试题解析
4. 下列计算正确的是（）

A、 $a^{3} \cdot a^{2} = a^{6}$ B、 ${(- 3 x^{2} y^{3})}^{2} = 6 x^{4} y^{6}$ C、 ${(- a^{2} b)}^{3} \div a^{5} b^{3} = - a$ D、 $m^{4} + m^{4} = m^{8}$

查看试题解析
5. 从正多边形的一个顶点可以引出5条对角线,则这个正多边形每个外角的度数为（）

A、135° B、45° C、60° D、120°

查看试题解析
6. 中华人民共和国成立70周年之际，美术社团的同学们用手中的画笔表达了对祖国的爱与祝福.活动中，他们先后两次购买画笔，第一次用120元购买了若干支，第二次用240元在同一家商店购买同样的画笔，这次商家每支优惠2元，结果购买画笔的数量恰好是第一次的3倍，求第一次买了多少支画笔?若设第一次买了x支画笔，根据题意，列方程正确的是（）

A、 $\frac{240}{3 x} - \frac{120}{x} = 2$ B、 $\frac{240}{x} - \frac{120}{3 x} = 2$ C、 $\frac{120}{3 x} - \frac{240}{x} = 2$ D、 $\frac{120}{x} - \frac{240}{3 x} = 2$

查看试题解析
7. 在数学活动课上，老师提出这样一个问题：“已知 $∠ M O N$ ，同学们只用一块三角板可以画出它的角平分线吗？”聪明的小阳经过思考设计了如下方案（如图）：
⑴在角的两边OM、ON上分别取OA=OB；

⑵过点A作DA⊥OM于点A，交ON于点D；过点B作EB⊥ON于点B，交OM于点E，AD、BE交于点C；

⑶作射线OC．

小阳接着解释说：“此时，△OAC≌△OBC，所以射线OC为∠MON的平分线。”小阳的方案中，△OAC≌△OBC的依据是（）

A、SAS B、ASA C、HL D、AAS

查看试题解析
8. 如图，在△ $A B C$ 中， $A B = A C$ ， $A D$ 、 $B E$ 分别是底边 $B C$ 和腰 $A C$ 上的中线，点 $P$ 为 $A D$ 上一动点，则 $P E + P C$ 的最小值等于（）

A、线段 $A B$ 的长 B、线段 $B C$ 的长 C、线段 $A D$ 的长 D、线段 $B E$ 的长

查看试题解析
9. 我国著名数学家华罗庚曾在给青少年撰写的“数学是我国人民擅长的学科”一文中谈到，我国古代数学的许多创新与发展都曾居世界前列.其中，我国南宋数学家在所著的《详解九章算术》（1261年）一书中就用上图解释了二项和的乘方规律.这位南宋数学家是（）

A、秦九韶 B、杨辉 C、祖冲之 D、赵爽

查看试题解析
10. 如图，已知△ $A B C$ ，按以下步骤作图：①分别以 $B$ 、 $C$ 为圆心，大于 $\frac{1}{2}$ $B C$ 的长为半径画弧，两弧交于点 $M$ 、 $N$ ；②作直线 $M N$ 交 $A B$ 于点 $D$ ，连接 $C D$ ，若 $C D = A D$ ，则下列结论中不一定成立的是（）

A、 $∠ A C B = 90 °$ B、△ $A C D$ 是等边三角形 C、点D是AB的中点 D、 $S_{Δ A C D} = S_{Δ B C D}$

查看试题解析

二、填空题

11. 若分式 $\frac{| x | - 2}{x + 2}$ 的值为0，则 $x$ 的值是．

查看试题解析
12. 如图所示， $a$ ∥ $b$ ， $∠ B A C = 90 °$ ， $∠ 1 = 10 °$ ， $∠ 2 = 50 °$ ，则 $∠ C$ 的度数为.

查看试题解析
13. 已知点 $M$ ( $m + 1$ ，1) 与点 $N$ （2， $n - 1$ ）关于 $y$ 轴对称，则 $n^{m}$ 的值为.

查看试题解析
14. 如图，在△ $A B C$ 中， $∠ A = 45 ° ， ∠ A C B = 75 ° ， B C = 5$ ，将△ $A B C$ 绕点C旋转得到△ $A' B' C$ ，且点 $B'$ 恰好落在AB边上，则 $B B'$ 的长为.

查看试题解析
15. 如图，△ $A B C$ 中， $A B = A C ， ∠ B A C = 45 ° ，$ AD、CE分别为△ABC的高，并交于点F，若 $B D = \frac{3}{2} c m$ ，则 $A F$ 的长为.

查看试题解析

三、解答题

16. 因式分解：

(1)、 $2 a^{2} - 8 b^{2}$

(2)、 $1 + (x - 1) (x - 3)$

查看试题解析
17.

(1)、计算: $(x + 4) (x - 4) - 3 (x^{2} - x + 1)$

(2)、解方程： $\frac{2}{x + 1} - \frac{3}{1 - x} = \frac{6}{x^{2} - 1}$

查看试题解析
18. 先化简,再求值: $\frac{x^{2} - 4}{x^{2} + 4 x + 4} \div (\frac{x^{2} - 3 x + 6}{x + 2} - 1)$ ，其中 $x = - 2$ .

查看试题解析
19. 已知：如图，点B，D在线段AE上，AD=BE，AC∥EH，∠C=∠H.求证：BC=DH.

查看试题解析
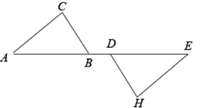20. 如图，已知∠AOB，点 $C$ 是边 $O A$ 上一点，且∠ACD=∠AOB．

(1)、尺规作图：作∠AOB的平分线OE，交CD于点E.（保留作图痕迹，不写作法）

(2)、在(1)所作图形中，若∠AOB=30°，OC=4，求△OCE的面积.

查看试题解析
21. 2019年8月．山西龙城将迎来全国第二届青年运动会，盛会将至，整个城市已经进入了全力准备的状态．太职学院足球场作为一个重要比赛场馆．占地面积约24300平方米．总建筑面积4790平方米，设有2476个座位，整体建筑简洁大方，独具特色.2018年3月15日该场馆如期开工，某施工队负责安装该场馆所有座位，在安装完476个座位后，采用新技术，效率比原来提升了25%．结来比原计划提前4天完成安装任务．求原计划每天安装多少个座位．

查看试题解析
22. 阅读下面材料，完成相应任务：

(1)、小明在研究命题①时，在图1的正方形网格中画出两个符合条件的四边形.由此判断命题①是命题(填“真”或“假”).

(2)、小彬经过探究发现命题②是真命题.请你结合图2证明这一命题.

(3)、小颖经过探究又提出了一个新的命题：“若 $A B = A' B'$ ， $B C = B' C'$ ， $C D = C' D'$ ，，，则四边形 $A B C D$ ≌四边形 $A' B' C' D'$ ”请在横线上填写两个关于“角”的条件，使该命题为真命题.

查看试题解析
23. 综合与实践
问题情境

在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， $C D ⊥ A B$ 于点 $D$ ，点 $E$ 是射线 $A B$ 上一点，连接 $C E$ ，过点 $B$ 作 $B F ⊥ C E$ 于点 $F$ ，且交直线 $C D$ 于点 $G$ .

(1)、如图1，当点 $E$ 在线段 $A D$ 上时，求证： $C G = A E$ .
自主探究

(2)、如图2，当点 $E$ 在线段 $B D$ 上时，其它条件不变，请猜想 $C G$ 与 $A E$ 之间的数量关系，并说明理由.
拓展延伸

(3)、如图3，当点 $E$ 在线段 $A B$ 的延长线上时，其它条件不变，请直接写出 $C G$ 与 $A E$ 之间的数量关系.

查看试题解析