山西省吕梁市交城县2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-13 类型：期末考试

进入出卷网下载

一、单选题

1. 小颖用长度为奇数的三根木棒搭一个三角形，其中两根木棒的长度分别为 $7 c m$ 和 $3 c m$ ，则第三根木棒的长度是（）

A、 $7 c m$ B、 $8 c m$ C、 $11 c m$ D、 $13 c m$

查看试题解析
2. 下列文化体育活动的图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如果等腰三角形的一个角是80°，那么它的底角是（）

A、80°或50° B、50°或20° C、80°或20° D、50°

查看试题解析
4. 若2x + m 与 x + 2 的乘积中不含的 x 的一次项，则m 的值为（）

A、－4 B、4 C、－2 D、2

查看试题解析
5. 如图所示的是用4个全等的小长方形与1个小正方形密铺而成的正方形图案，已知该图案的面积为144，小正方形的面积为4，若分别用x、y（ $x > y$ ）表示小长方形的长和宽，则下列关系式中错误的是（）

A、 $x^{2} + y^{2} = 100$ B、 $x - y = 2$ C、 $x + y = 12$ D、 $x y = 35$

查看试题解析
6. 若关于 $x$ 的分式方程 $\frac{x + m}{4 - x^{2}} + \frac{x}{x - 2} = 1$ 无解，则m的值是（）

A、 $m = 2$ 或 $m = 6$ B、 $m = 2$ C、 $m = 6$ D、 $m = 2$ 或 $m = - 6$

查看试题解析
7. “绿水青山就是金山银山”，为了加大深圳城市森林覆盖率，市政府决定在2019年3月12日植树节前植树2000棵，在植树400棵后，为了加快任务进程，采用新设备，植树效率比原来提升了25%，结果比原计划提前5天完成所有计划，设原计划每天植树x棵，依题意可列方程（）

A、 $\frac{2000}{x} - \frac{2000}{x (1 + 25 %)} = 5$ B、 $\frac{2000 - 400}{x (1 + 25 %)} - \frac{2000 - 400}{x} = 5$ C、 $\frac{2000}{x} - \frac{2000 - 400}{x (1 + 25 %)} = 5$ D、 $\frac{2000 - 400}{x} - \frac{2000 - 400}{x (1 + 25 %)} = 5$

查看试题解析
8. 如图，点D在AB上，点E在AC上，AB＝AC添加下列一个条件后，还不能证明△ABE≌△ACD的是（）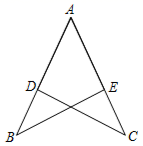

A、AD＝AE B、BD＝CE C、∠B＝∠C D、BE＝CD

查看试题解析
9. 如图，在△ABC中，∠CAB＝90°，∠ABC＝60°，BD平分∠ABC，若CD＝6，则AD的长为（）

A、2 B、3 C、4 D、4.5

查看试题解析
10. 如图，∠AOB=60°，OA=OB，动点C从点O出发，沿射线OB方向移动，以AC为边在右侧作等边△ACD，连接BD，则BD所在直线与OA所在直线的位置关系是（）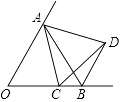

A、平行 B、相交 C、垂直 D、平行、相交或垂直

查看试题解析

二、填空题

11. 使分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，这时x= ．

查看试题解析
12. 已知 $2^{32} - 1$ 可以被10到20之间某两个整数整除，则这两个数是．

查看试题解析
13. 目前世界上能制造的芯片最小工艺水平是5纳米,而我国能制造芯片的最小工艺水平是16纳米,已知1纳米= $10^{- 9}$ 米,用科学记数法将16纳米表示为米.

查看试题解析
14. 如图，△ABC≌△DEC，其中AB与DE是对应边，AC与DC是对应边，若∠A=∠30°，∠CEB=70°，则∠ACD=°.

查看试题解析
15. 有一程序，如果机器人在平地上按如图所示的步骤行走，那么机器人回到A点处行走的路程是．

查看试题解析
16. 已知：如图，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA，过E作EF⊥AB，F为垂足，下列结论：①△ABD≌△EBC；②∠BCE+∠BCD=180°；③AD=EF=EC；④AE=EC，其中正确的是(填序号)

查看试题解析

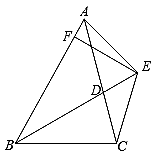
三、解答题

17. 计算下列各题．

(1)、（x²+3）（3x²﹣1）

(2)、（4x²y﹣8x³y³）÷（﹣2x²y）

(3)、[（m+3）（m﹣3）]²

(4)、10^﹣2×10⁰+10⁵÷10³

(5)、 ${(\frac{3 x}{4 y})}^{2} \cdot \frac{2 y}{3 x} + \frac{x}{2 y^{2}} \cdot \frac{2 y}{x}$

(6)、 $(1 - \frac{3}{x + 2}) \div \frac{x - 1}{x^{2} + 2 x} - \frac{x}{x + 1}$ ，其中x满足x²﹣x﹣1＝0．

查看试题解析
18. 解方程．

(1)、 $\frac{4}{x^{2} - 4} + \frac{x + 3}{x - 2} = \frac{x - 1}{x + 2}$

(2)、 $\frac{1}{x - 3} + 2 = \frac{4 - x}{3 - x}$

查看试题解析
19. 如图，在下列带有坐标系的网格中，△ABC的顶点都在边长为1的小正方形的顶点上

(1)、直接写出坐标：A ， B

(2)、画出△ABC关于y轴的对称的△DEC（点D与点A对应）

(3)、用无刻度的直尺，运用全等的知识作出△ABC的高线BF（保留作图痕迹）

查看试题解析
20. 仔细阅读下面例题，解答问题.
（例题）已知关于 $x$ 的多项式 $x^{2} - 4 x + m$ 有一个因式是 $(x + 3)$ ，求另一个因式及 $m$ 的值.

解：设另一个因式为 $(x + n)$ ，

则 $x^{2} - 4 x + m = (x + 3) (x + n)$ ，即 $x^{2} - 4 x + m = x^{2} + (n + 3) x + 3 n$ .

$∴ {\begin{array}{l} n + 3 = - 4 ， \\ 3 n = m . \end{array}$ 解得 ${\begin{array}{l} m = - 21 ， \\ n = - 7. \end{array}$

∴另一个因式为 $(x - 7)$ ， $m$ 的值为 $- 21$ .

（问题）仿照以上方法解答下面问题：

(1)、已知关于 $x$ 的多项式 $x^{2} + 7 x + a$ 有一个因式是 $(x - 2)$ ，求另一个因式及 $a$ 的值.

(2)、已知关于 $x$ 的多项式 $2 x^{2} + 3 x - k$ 有一个因式是 $(x + 4)$ ，求 $k$ 的值.

查看试题解析
21. 如图，在直角三角形ABC中，∠ACB＝90°，∠B＝60°，AD ， CE是角平分线，AD与CE相交于点F ， FM⊥AB ， FN⊥BC ，垂足分别为M ， N.求证：FE＝FD．

查看试题解析
22. 因汽车尾气污染引发的雾霾天气备受关注，经市大气污染防治工作领导组研究决定，在市区范围实施机动车单双号限行措施限行期间为方便市民出行，某路公交车每天比原来的运行增加20车次．经调研得知，原来这路公交车平均每天共运送乘客5600人，限行期间这路公交车平均每天共运送乘客7000人，且平均每车次运送乘客与原来的数量基本相同，问限行期间这路公交车每天运行多少车次？

查看试题解析
23. 如图1，在△ABC和△ADE中，∠BAC＝∠EAD，AB＝AC，AD＝AE，连接CD、AE交于点F．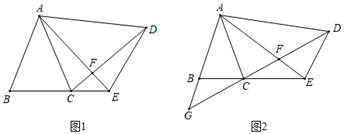

(1)、求证：BE＝CD．

(2)、当∠BAC＝∠EAD＝30°，AD⊥AB时（如图2），延长DC、AB交于点G，请直接写出图中除△ABC、△ADE以外的等腰三角形．

查看试题解析