山西省临汾市侯马市2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-13 类型：期末考试

进入出卷网下载

一、单选题

1. 在下面数据中，无理数是（）

A、 $\sqrt[3]{5}$ B、 $\sqrt{16}$ C、 $\frac{20}{3}$ D、0.585858…

查看试题解析
2. 下列运算正确的是（）

A、 $x^{3} \cdot x^{4} = x^{12}$ B、 ${(x^{3})}^{4}$ = $x^{12}$ C、 $x^{6} \div x^{2} = x^{3}$ D、 ${(3 b^{3})}^{2} = 6 b^{6}$

查看试题解析
3. 将下列长度的三根木棒首尾顺次连接，不能组成直角三角形的是（）

A、7、24、25 B、5、12、13 C、3、4、5 D、2、3、 $\sqrt{7}$

查看试题解析
4. 如图，在△ABC中，AB＝AC，D是BC的中点，AC的垂直平分线交AC，AD，AB于点E，O，F，则图中全等三角形的对数是（）

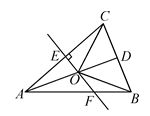A、1对 B、2对 C、3对 D、4对

查看试题解析
5. 某班共有学生40人，其中10月份生日的学生人数为8人，则10月份生日学生的频数和频率分别为（）

A、10和25% B、25%和10 C、8和20% D、20%和8

查看试题解析
6. 若（x+m）（x﹣8）中不含x的一次项，则m的值为（）

A、8 B、﹣8 C、0 D、8或﹣8

查看试题解析
7. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，请你根据所学的图形的全等这一章的知识，说明画出∠A′O′B′=∠AOB的依据是（）

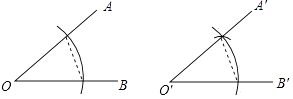A、SAS B、ASA C、AAS D、SSS

查看试题解析
8. 牛顿曾说过：“反证法是数学家最精良的武器之一．”那么我们用反证法证明：“在一个三角形中，至少有一个内角小于或等于60°”时，第一步先假设（）

A、三角形中有一个内角小于60° B、三角形中有一个内角大于60° C、三角形中每个内角都大于60° D、三角形中没有一个内角小于60°

查看试题解析
9. 下列各命题的逆命题中，①三个角对应相等的两个三角形是全等三角形；②全等三角形对应边上的高相等；③全等三角形的周长相等；④两边及其中一边的对角对应相等的两个三角形是全等三角形；假命题是（）

A、①② B、①③ C、②③ D、①④

查看试题解析
10.
如图是油路管道的一部分，延伸外围的支路恰好构成一个直角三角形，两直角边分别为3m和4m．按照输油中心O到三条支路的距离相等来连接管道，则O到三条支路的管道总长（计算时视管道为线，中心O为点）是（　　）

A、2m B、3m C、4m D、6m

查看试题解析

二、填空题

11. $- 8$ 的立方根是．

查看试题解析
12. 若多项式 $x^{2} + m x + 9$ 是一个完全平方式，则 $m =$ .

查看试题解析
13. 如图，某会展中心在会展期间准备将高5m，长13m，宽2m的楼道上铺地毯，已知地毯每平方米18元，请你帮助计算一下，铺完这个楼道至少需要元钱．

查看试题解析
14. 我国宋朝数学家杨辉在他的著作《详解九章算法》中提出如图，此表揭示了（a+b）ⁿ（n为非负整数）展开式的各项系数的规律，例如：（a+b）⁰＝1，它只有一项，系数为1；（a+b）¹＝a+b，它有两项，系数分别为1，1；（a+b）²＝a²+2ab+b² ，它有三项，系数分别为1，2，1；（a+b）³＝a³+3a²b+3ab²+b³ ，它有四项，系数分别为1，3，3，1；…；根据以上规律，（a+b）⁵展开式共有六项，系数分别为，拓展应用：（a﹣b）⁴＝．

查看试题解析
15. 在底面直径为3cm，高为3cm的圆柱体侧面上，用一条无弹性的丝带从A至C按如图所示的圈数缠绕，则丝带的最短长度为cm．（结果保留π）

查看试题解析

三、解答题

16. 对下列代数式分解因式

(1)、n²（m﹣2）﹣n（2﹣m）；

(2)、（x﹣1）（x﹣3）+1．

查看试题解析
17.

(1)、计算：2（m+1）²﹣（2m+1）（2m﹣1）；

(2)、先化简，再求值.[（x+2y）²﹣（x+y）（3x﹣y）﹣5y²]÷2x，其中x＝﹣2，y＝ $\frac{1}{2}$ ．

查看试题解析
18. 如图，已知∠AOB和点C，D．
求作：点P，使得点P到∠AOB两边的距离相等，且PC＝PD．（要求：用直尺与圆规作图，保留作图痕迹）

查看试题解析
19. 某校为了进一步丰富学生的课外阅读，欲增购一些课外书，为此对该校一部分学生进行了一次“你最喜欢的书籍”问卷调查（每人只选一项）．根据收集到的数据，绘制成如下统计图（不完整）：
请根据图中提供的信息，完成下列问题：

(1)、在这次问卷调查中，一共抽查了名学生；并在图中补全条形统计图；

(2)、如果全校共有学生1600名，请估计该校最喜欢“科普”书籍的学生约有多少人？

查看试题解析
20. 如图，△ABC中，D是BC上的一点．若AB＝10，BD＝6，AD＝8，AC＝17，求△ABC的面积．

查看试题解析
21. 如图，△ABC和△ADE都是等腰直角三角形，CE与BD相交于点M，BD交AC于点N.

(1)、证明：BD＝CE；

(2)、证明：BD⊥CE．

查看试题解析
22. 如图，已知 $△ A B C$ 中， $A B = A C = 10 c m$ ， $B C = 8 c m$ ，点 $D$ 为 $A B$ 的中点，如果点 $P$ 在线段 $B C$ 上以 $3 c m / s$ 的速度由点 $B$ 向点 $C$ 运动，同时，点 $Q$ 在线段 $C A$ 上由点 $C$ 向点 $A$ 运动.

(1)、若点 $Q$ 与点 $P$ 的运动速度相等，经过1秒后， $△ B P D$ 与 $△ C Q P$ 是否全等？请说明理由；

(2)、若点 $Q$ 与点 $P$ 的运动速度不相等，当点 $Q$ 的运动速度为多少时，能使 $△ B P D$ 与 $△ C Q P$ 全等？

查看试题解析
23. 综合与探究

(1)、操作发现：如图1，点D是等边△ABC边BA上一动点（点D与点B不重合），连结DC，以DC为边在CD上方作等边△DCF，连结AF，你能发现线段AF与BD之间的数量关系吗？证明你发现的结论．

(2)、类比猜想：如图2，当动点D运动至等边△ABC边BA的延长线上时，其余条件不变，猜想：（1）中的结论是否成立，并说明理由．

(3)、拓展探究：如图3.当动点D在等边△ABC边BA上运动时（点D与点B不重合），连结DC，以DC为边在CD上方和下方分别作等边△DCF和等边△DCF′，连结AF，BF′，探究：AF、BF′与AB有何数量关系？并说明理由．

查看试题解析