山西省大同市2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-13 类型:期末考试
一、单选题
-
1. 下图的四个古汉字中,不是轴对称图形的是( )A、
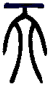 B、
B、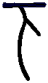 C、
C、 D、
D、 2. 点 关于 轴对称的点的坐标是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 若一个多边形的内角和小于其外角和,则这个多边形的边数是()A、3 B、4 C、5 D、65. 2019年5月24日,中国·大同石墨烯+新材料储能产业园正式开工,这是大同市争当能源革命“尖兵”的又一重大举措.石墨烯是已知强度最高的材料之一,同时还具有很好的韧性,石墨烯的理论厚度为0.00000000034米,这个数据用科学记数法可表示为( )A、 B、 C、 D、6. 若分式 的值为0,则x的值为( )A、0 B、1 C、﹣1 D、±17. 已知 是完全平方式,则m的值为( )A、6 B、 C、 D、248. 用三角尺可按下面方法画角平分线:在已知∠AOB两边上分别取OM=ON , 再分别过点M , N作OA,OB的垂线,两垂线交于点P , 画射线OP , 则OP平分∠AOB . 作图过程用到了△OPM≌△OPN , 那么△OPM≌△OPN所用的判定定理是( )
2. 点 关于 轴对称的点的坐标是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 若一个多边形的内角和小于其外角和,则这个多边形的边数是()A、3 B、4 C、5 D、65. 2019年5月24日,中国·大同石墨烯+新材料储能产业园正式开工,这是大同市争当能源革命“尖兵”的又一重大举措.石墨烯是已知强度最高的材料之一,同时还具有很好的韧性,石墨烯的理论厚度为0.00000000034米,这个数据用科学记数法可表示为( )A、 B、 C、 D、6. 若分式 的值为0,则x的值为( )A、0 B、1 C、﹣1 D、±17. 已知 是完全平方式,则m的值为( )A、6 B、 C、 D、248. 用三角尺可按下面方法画角平分线:在已知∠AOB两边上分别取OM=ON , 再分别过点M , N作OA,OB的垂线,两垂线交于点P , 画射线OP , 则OP平分∠AOB . 作图过程用到了△OPM≌△OPN , 那么△OPM≌△OPN所用的判定定理是( )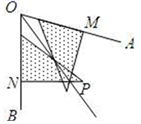 A、SSS B、SAS C、HL D、ASA9. 解分式方程 时,在方程两边同乘 ,把原方程化为:2x-(x+1)=1,这一变形过程体现的数学思想主要是( )A、类比思想 B、转化思想 C、方程思想 D、函数思想10. 如图,在 中, 平分 , ,且分别交 , , 及 的延长线于点 , , , ,若 , ,则 的度数为( )
A、SSS B、SAS C、HL D、ASA9. 解分式方程 时,在方程两边同乘 ,把原方程化为:2x-(x+1)=1,这一变形过程体现的数学思想主要是( )A、类比思想 B、转化思想 C、方程思想 D、函数思想10. 如图,在 中, 平分 , ,且分别交 , , 及 的延长线于点 , , , ,若 , ,则 的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若x2n=2,则x6n= .
12. 若 ,则 .13. 已知等腰三角形的两边长分别为4和8,则它的周长是 .14. 已知 ,则 的值为.15. 如图,等边△ABC 中,E 是 AC 边的中点,AD 是 BC 边上的中线,P是 AD 上的动点,若 AD=6,则 EP+CP 的最小值为 .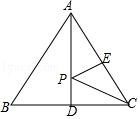
三、解答题
-
16. 计算:(1)、(2)、 .17. 分解因式:(1)、 ;(2)、 .18. 先化简,再求值: ,其中 .19. 如图,已知 是 的外角,
 (1)、作 的平分线 (尺规作图,不写作法,保留作图痕迹);(2)、在(1)的基础上,若 ,求证: .20. 为了全面推进青少年素质教育,我市某中学组织八年级学生前往距学校 的“示范性综合实践基地”开展社会实践活动.一部分学生骑自行车先走,过了 后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.21. 如图,在 中, , , 的垂直平分线 交 于点 ,交 于点 ,若 ,求 的长.
(1)、作 的平分线 (尺规作图,不写作法,保留作图痕迹);(2)、在(1)的基础上,若 ,求证: .20. 为了全面推进青少年素质教育,我市某中学组织八年级学生前往距学校 的“示范性综合实践基地”开展社会实践活动.一部分学生骑自行车先走,过了 后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.21. 如图,在 中, , , 的垂直平分线 交 于点 ,交 于点 ,若 ,求 的长.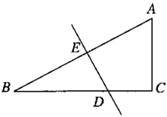 22. 阅读下列材料,并完成相应的任务:
22. 阅读下列材料,并完成相应的任务:杨辉三角
我国著名数学家华罗庚曾在给青少年撰写的“数学是我国人民所擅长的学科”一文中谈到,我国古代数学的许多创新与发展都曾居世界前列,他说:“实际上我们祖国伟大人民在人类史上,有过无比睿智的成就.”其中“杨辉三角”就是一例.
在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,给出了二项式 的展开式(按 的次数由大到小的顺序排列)及其系数规律.
如图所示
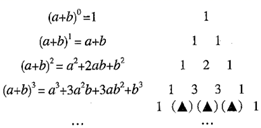
任务:
(1)、通过观察,图中的(▲)中可填入的数字依次为、、;(2)、请直接写出 的展开式: ;(3)、根据(2)中的规律,求 的值,写出计算过程.23. 综合与实践问题情境
如图1, 和 均为等边三角形,点 , , 在同一条直线上,连接 ;
 (1)、探究发现
(1)、探究发现善思组发现: ,请你帮他们写出推理过程;
(2)、钻研组受善思组的启发,求出了 度数,请直接写出 等于度;(3)、奋进组在前面两组的基础上又探索出了 与 的位置关系为(请直接写出结果);(4)、拓展探究如图2, 和 均为等腰直角三角形, ,点 , , 在同一条直线上, 为 中 边上的高,连接 ,试探究 , , 之间有怎样的数量关系.

创新组类比善思组的发现,很快证出 ,进而得出 .请你写出 , , 之间的数量关系并帮创新组完成后续的证明过程.