内蒙古自治区通辽市开鲁县2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-13 类型：期末考试

进入出卷网下载

一、单选题

1. 点M（﹣2，1）关于x轴的对称点N的坐标是（　　）

A、（2，1） B、（﹣2，1） C、（﹣2，﹣1） D、（2，﹣1）

查看试题解析
2. 使分式 $\frac{x - 3}{2 x - 1}$ 有意义的x的取值范围是（）

A、x＞ $\frac{1}{2}$ B、x＜ $\frac{1}{2}$ C、x≠3 D、x≠ $\frac{1}{2}$

查看试题解析
3. 如图，已知 $∠ A B C = ∠ D C B$ ，添加以下条件，不能判定 $Δ A B C ≅ Δ D C B$ 的是（）

A、 $A B = D C$ B、 $B E = C E$ C、 $A C = D B$ D、 $∠ A = ∠ D$

查看试题解析
4. 长度单位1纳米=10^-9米，目前发现一种新型禽流感病毒（H7N9）的直径约为101纳米，用科学记数法表示该病毒直径是（）

A、10.1×10^-8米 B、1.01×10^-7米 C、1.01×10^-6米 D、0.101×10^-6米

查看试题解析
5. 计算结果为x²﹣y²的是（）

A、（﹣x+y）（﹣x﹣y） B、（﹣x+y）（x+y） C、（x+y）（﹣x﹣y） D、（x﹣y）（﹣x﹣y）

查看试题解析
6. 如图，已知D为△ABC边AB的中点，E在AC上，将△ABC沿着DE折叠，使A点落在BC上的F处．若∠B=65°，则∠BDF等于（）

A、65° B、50° C、60° D、57.5°

查看试题解析
7. 若（x+a）（x²﹣x﹣b）的乘积中不含x的二次项和一次项，则常数a、b的值为（）

A、a＝1，b＝﹣1 B、a＝﹣1，b＝1 C、a＝1，b＝1 D、a＝﹣1，b＝﹣1

查看试题解析
8. 一项工程，甲单独做需要m天完成，乙单独做需要n天完成，则甲、乙合作完成工程需要的天数为（）

A、m+n B、 $\frac{m + n}{2}$ C、 $\frac{m n}{m + n}$ D、 $\frac{m + n}{m n}$

查看试题解析
9. “绿水青山就是金山银山”．某工程队承接了60万平方米的荒山绿化任务，为了迎接雨季的到来，实际工作时每天的工作效率比原计划提高了25%，结果提前30天完成了这一任务．设实际工作时每天绿化的面积为x万平方米，则下面所列方程中正确的是（）

A、 $\frac{60}{x} - \frac{60}{(1 + 25 %) x} = 30$ B、 $\frac{60}{(1 + 25 %) x} - \frac{60}{x} = 30$ C、 $\frac{60 \times (1 + 25 %)}{x} - \frac{60}{x} = 30$ D、 $\frac{60}{x} - \frac{60 \times (1 + 25 %)}{x} = 30$

查看试题解析
10. 如图，是用4个相同的小长方形与1个小正方形镶嵌而成的正方形图案，已知图案的面积为25，小正方形的面积为9，若用x，y长示小长方形的两边长(x>y)请观察图案，以下关系式中错误的是（）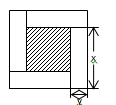

A、x²+y²=16 B、x-y=3 C、4xy+9=25 D、x+y=5

查看试题解析

二、填空题

11. 约分： $\frac{- 25 a^{2} b c^{3}}{15 a b^{2} c} =$ ．

查看试题解析
12. 若 $4 x^{2} + m x + 9$ 是一个完全平方式，则m的值是．

查看试题解析
13. 已知m+2n+2＝0，则2^m•4ⁿ的值为．

查看试题解析
14. 如图，△ABC的两条高BD、CE相交于点O 且OB＝OC ．则下列结论：
①△BEC≌△CDB；

②△ABC是等腰三角形；

③AE＝AD；

④点O在∠BAC的平分线上，

其中正确的有．（填序号）

查看试题解析
15. 如图，在正方形网格中有两个小正方形被涂黑，再涂黑一个图中其余的小正方形，使得整个被涂黑的图案构成一个轴对称图形，那么涂法共有种.

查看试题解析
16. 如图，在△ABC中∠ABC和∠ACB平分线交于点O ，过点O作OD⊥BC于点D ， △ABC的周长为21，OD＝4，则△ABC的面积是．

查看试题解析
17. 若关于x的方程 $\frac{1}{x - 4}$ + $\frac{m}{x + 4}$ = $\frac{m + 3}{x^{2} - 16}$ 无解，则m的值为．

查看试题解析

三、解答题

18. 计算：

(1)、18x³yz•（﹣ $\frac{1}{3}$ y²z）³÷ $\frac{1}{6}$ x²y²z

(2)、 ${(\frac{3 x}{4 y})}^{2} • \frac{2 y}{3 x} + \frac{x^{2}}{2 y^{2}}$ ÷ $\frac{2 y^{2}}{x}$

查看试题解析
19. 先化简，再求值：
[（2x﹣y）²+（2x﹣y）（2x+y）+8xy]÷4x ，其中x＝﹣ $\frac{1}{2}$ ，y＝4

查看试题解析
20. 先化简，再求值：
（1﹣ $\frac{3}{a + 2}$ ）÷ $\frac{a^{2} - 2 a + 1}{a^{2} - 4}$ ，其中a＝（3﹣π）⁰+（ $\frac{1}{4}$ ）^﹣1 ．

查看试题解析
21. 解分式方程： $\frac{2 x}{x + 1} + \frac{3}{x - 1} = 2$ ．

查看试题解析
22. 因式分解：

(1)、﹣3x³y²+6x²y³﹣3xy⁴

(2)、9a²（x﹣y）+4b²（y﹣x）

查看试题解析
23. 一辆汽车开往距离出发地240km的目的地，出发后第一小时内按原计划的速度匀速行驶，一小时后以原来速度的1.5倍匀速行驶，并比原计划提前40min到达目的地，求前一小时的行驶速度．

查看试题解析
24. 在△ABC中，AB＝AC ， ∠BAC＝120°，AD⊥BC ，垂足为G ，且AD＝AB ， ∠EDF＝60°，其两边分别交边AB ， AC于点E ， F ．

(1)、连接BD ，求证：△ABD是等边三角形；

(2)、试猜想：线段AE、AF与AD之间有怎样的数量关系？并给以证明．

查看试题解析
25. 探究下面的问题：

(1)、如图甲，在边长为a的正方形中去掉一个边长为b的小正方形(a＞b)，把余下的部分剪拼成如图乙的一个长方形，通过计算两个图形(阴影部分)的面积，验证了一个等式，这个等式是(用式子表示)，即乘法公式中的公式.

(2)、运用你所得到的公式计算：
①10.7×9.3

② $(x + 2 y - 3 z) (x - 2 y - 3 z)$

查看试题解析
26. 阅读材料：若m²﹣2mn+2n²﹣10n+25＝0，求m ， n的值．
解：∵m²﹣2mn+2n²﹣10n+25＝0，

∴（m²﹣2mn+n²）+（n²﹣10n+25）＝0．

∴（m﹣n）²+（n﹣5）²＝0，

∴m﹣n＝0，n﹣5＝0．

∴n＝5，m＝5．

根据你的观察，探究下面的问题：

(1)、已知：x²+2xy+2y²+4y+4＝0，求x^y的值；

(2)、已知：△ABC的三边长a ， b ， c都是正整数，且满足：a²+b²﹣16a﹣12b+100＝0，求△ABC的周长的最大值；

(3)、已知：△ABC的三边长是a ， b ， c ，且满足：a²+2b²+c²﹣2b（a+c）＝0，试判断△ABC是什么形状的三角形并说明理由．

查看试题解析