内蒙古通辽市奈曼旗2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-13 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算，正确的是（）

A、 $x^{m} + x^{m} = x^{2 m}$ B、 $2 x^{n} - x^{n} = 2$ C、 $x^{3} \cdot x^{3} = 2 x^{3}$ D、 $x^{2} \div x^{6} = x^{- 4}$

查看试题解析
2. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，则x的值为（）

A、0 B、1 C、﹣1 D、±1

查看试题解析
3. 下列式子中，从左到右的变形是因式分解的是（）．

A、(x－1)(x－2)＝x²－3x＋2 B、x²－3x＋2＝(x－1)(x－2) C、x²＋4x＋4＝x(x一4)＋4 D、x²＋y²＝(x＋y)(x—y)

查看试题解析
4. 国际数学家大会的会标如图1所示，把这个图案沿图中线段剪开后能拼成如图2所示的四个图形，则其中是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 某人到瓷砖商店去购买一种多边形形状的瓷砖，用来铺设无缝地板，他购买的瓷砖形状不可以是（）

A、正三角形 B、矩形 C、正八边形 D、正六边形

查看试题解析
6. 如图，AC∥BD，AD与BC相交于O，∠A＝45°，∠B＝30°，那么∠AOB等于（）

A、75° B、60° C、45° D、30°

查看试题解析
7. 如图，C、E和B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是（）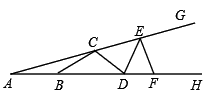

A、80° B、90° C、100° D、108°

查看试题解析
8. 如图，把 $Δ A B C$ 纸片沿 $D E$ 折叠，当点 $A$ 落在四边形 $B C D E$ 内部时，则 $∠ A$ 与 $∠ 1 + ∠ 2$ 之间有一种数量关系始终保持不变，试着找一找这个规律你发现的规律是（）

A、 $∠ 1 + ∠ 2 = 2 ∠ A$ B、 $∠ 1 + ∠ 2 = ∠ A$ C、 $∠ A = 2 (∠ 1 + ∠ 2)$ D、 $∠ 1 + ∠ 2 = \frac{1}{2} ∠ A$

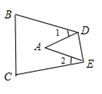查看试题解析
9. 若a+b=3，ab=2，则a²+b²的值是（）

A、2.5 B、5 C、10 D、15

查看试题解析
10. 篆刻是中国独特的传统艺术，篆刻出来的艺术品叫印章．印章的文字刻成凸状的称为“阳文”，刻成凹状的称为“阴文”．如图所示的“希望”即为阳文印章在纸上盖出的效果，此印章是下列选项中的（阴影表示印章中的实体部分，白色表示印章中的镂空部分）（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 使分式 $\frac{3 - 4 x}{x^{2} + 1}$ 的值是负数 $x$ 的取值范围是．

查看试题解析
12. 计算 $4 x^{2} y \cdot (- \frac{1}{4} x)$ = ．

查看试题解析
13. 木工师傅做完房门后，为防止变形，会在门上钉上一条斜拉的木条，这样做的根据是．

查看试题解析
14. 已知，如图，AD=AC，BD=BC，O为AB上一点，那么图中共有对全等三角形．

查看试题解析
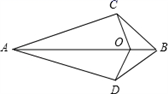15. 将一张长方形纸片按如图5所示的方式折叠，BC、BD为折痕，则∠CBD为度.

查看试题解析
16. 如果点 $P (4, - 5)$ 和点 $Q (a, b)$ 关于 $y$ 轴对称，则 ${(a - b)}^{2019} =$ ．

查看试题解析
17. 如图1，将边长为a的大正方形剪去一个边长为b的小正方形（a $>$ b），将剩下的阴影部分沿图中的虚线剪开，拼接后得到图2，这种变化可以用含字母a ， b的等式表示为．

查看试题解析

三、解答题

18. 计算：

(1)、 ${(2 a b^{2} c^{- 3})}^{- 2} \div {(a^{- 2} b)}^{3}$

(2)、 $\frac{a - 1}{a^{2} - 4 a + 4} \div \frac{a - 1}{a^{2} - 4}$

查看试题解析
19. 已知 $x = \sqrt{2} + 1$ ，求 $(\frac{x + 1}{x^{2} - x} - \frac{x}{x^{2} - 2 x + 1}) \div \frac{1}{x}$ 的值．

查看试题解析
20. 解方程： $\frac{2 x}{2 x - 1} + \frac{5}{1 - 2 x}$ ＝3.

查看试题解析
21. 如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．

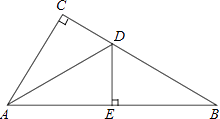(1)、求证：△ACD≌△AED；

(2)、若∠B=30°，CD=1，求BD的长．

查看试题解析
22. 在边长为的小正方形组成的正方形网格中建立如图所示的平面直角坐标系，已知格点三角形 $A B C$ （三角形的三个顶点都在小正方形的顶点上）

(1)、写出 $Δ A B C$ 的面积；

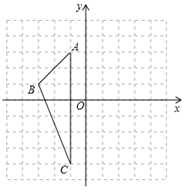(2)、画出 $Δ A B C$ 关于 $y$ 轴对称的 $Δ A_{1} B_{1} C_{1}$ ；

(3)、写出点 $A$ 及其对称点 $A_{1}$ 的坐标．

查看试题解析
23. 某县为了落实中央的“强基惠民工程”，计划将某村的居民自来水管道进行改造．该工程若由甲队单独施工恰好在规定时间内完成；若乙队单独施工，则完成工程所需天数是规定天数的1.5倍．如果由甲、乙队先合做15天，那么余下的工程由甲队单独完成还需5天．

(1)、这项工程的规定时间是多少天？

(2)、已知甲队每天的施工费用为6500元，乙队每天的施工费用为3500元．为了缩短工期以减少对居民用水的影响，工程指挥部最终决定该工程由甲、乙队合做来完成．则该工程施工费用是多少？

查看试题解析
24. 猜想与证明：小强想证明下面的问题：“有两个角（图中的 $∠ B$ 和 $∠ C$ ）相等的三角形是等腰三角形”．但他不小心将图弄脏了，只能看见图中的 $∠ C$ 和边 $B C$ ．

(1)、请问：他能够把图恢复成原来的样子吗？若能，请你帮他写出至少两种以上恢复的方法并在备用图上恢复原来的样子．

(2)、你能够证明这样的三角形是等腰三角形吗？（至少用两种方法证明）

查看试题解析
25. 在学习轴对称的时候，老师让同学们思考课本中的探究题．

如图（1），要在燃气管道l上修建一个泵站，分别向A、B两镇供气．泵站修在管道的什么地方，可使所用的输气管线最短？

你可以在l上找几个点试一试，能发现什么规律？你可以在 $l$ 上找几个点试一试，能发现什么规律？

聪明的小华通过独立思考，很快得出了解决这个问题的符合题意办法．他把管道l看成一条直线（图（2）），问题就转化为，要在直线l上找一点P，使AP与BP的和最小．他的做法是这样的：

①作点B关于直线l的对称点B′．

②连接AB′交直线l于点P，则点P为所求．

请你参考小华的做法解决下列问题．如图在△ABC中，点D、E分别是AB、AC边的中点，BC=6，BC边上的高为4，请你在BC边上确定一点P，使△PDE得周长最小．

(1)、在图中作出点P（保留作图痕迹，不写作法）．

(2)、请直接写出△PDE周长的最小值：

查看试题解析