内蒙古赤峰市林西县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-13 类型:期末考试
一、单选题
-
1. 下列图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中,不具有稳定性的是( )
2. 下列图形中,不具有稳定性的是( )
A、 B、
B、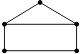 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 若分式 的值为0,则y的值是( )A、 B、 C、 D、5. 下列因式分解正确的是( )A、 B、 C、 D、6. 如图,在 中,AB=8,BC=6,AB、BC边上的高CE、AD交于点H,则AD与CE的比值是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 若分式 的值为0,则y的值是( )A、 B、 C、 D、5. 下列因式分解正确的是( )A、 B、 C、 D、6. 如图,在 中,AB=8,BC=6,AB、BC边上的高CE、AD交于点H,则AD与CE的比值是( )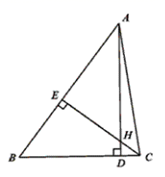 A、 B、 C、 D、7. 一个三角形的两边长为3和9,第三边长为偶数,则第三边长为( )A、6或8 B、8或10 C、8 D、108. 如图,BC=EC,∠BCE=∠DCA,要使△ABC≌△DEC,不能添加下列选项中的( )
A、 B、 C、 D、7. 一个三角形的两边长为3和9,第三边长为偶数,则第三边长为( )A、6或8 B、8或10 C、8 D、108. 如图,BC=EC,∠BCE=∠DCA,要使△ABC≌△DEC,不能添加下列选项中的( )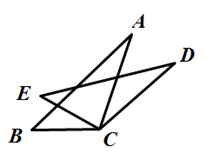 A、∠A=∠D B、AC=DC C、AB=DE D、∠B=∠E9. 计算 的结果是( )A、 B、 C、 D、10. 若 ,则m,n的值分别为( )A、 B、 C、 D、11. 从边长为 的正方形内去掉一个边长为b的小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证的等式是( )
A、∠A=∠D B、AC=DC C、AB=DE D、∠B=∠E9. 计算 的结果是( )A、 B、 C、 D、10. 若 ,则m,n的值分别为( )A、 B、 C、 D、11. 从边长为 的正方形内去掉一个边长为b的小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证的等式是( )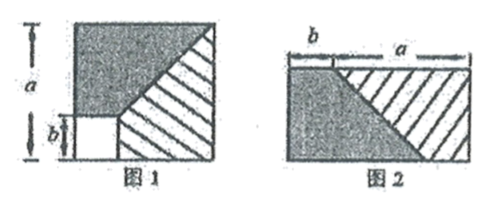 A、 B、 C、 D、12. 如图,牧童在A处放牛,其家在B处,A,B到海岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是( )
A、 B、 C、 D、12. 如图,牧童在A处放牛,其家在B处,A,B到海岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是( )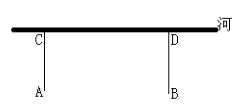 A、750 米 B、1500米 C、500 米 D、1000米13. 如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=125°,那么∠ABE的度数为( )
A、750 米 B、1500米 C、500 米 D、1000米13. 如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=125°,那么∠ABE的度数为( )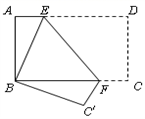 A、15° B、20° C、25° D、30°14. 如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为边并且在AB的同一侧作等边△ACD和等边△BCE , 连接AE交CD于M , 连接BD交CE于N . 给出以下三个结论:①AE=BD ; ②CN=CM; ③MN∥AB; ④∠CDB=∠NBE . 其中正确结论的个数是( )
A、15° B、20° C、25° D、30°14. 如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为边并且在AB的同一侧作等边△ACD和等边△BCE , 连接AE交CD于M , 连接BD交CE于N . 给出以下三个结论:①AE=BD ; ②CN=CM; ③MN∥AB; ④∠CDB=∠NBE . 其中正确结论的个数是( )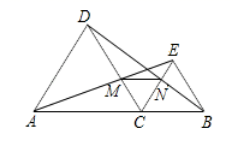 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
15. 等腰三角形的一个角是72º,则它的底角是 .16. 已知 , ,则 的值是 .17. 如果一个多边形的内角和为1260º,那么从这个多边形的一个顶点引对角线,可以把这个多边形分成个三角形.18. 某童装店销售一种童鞋,每双售价80元.后来,童鞋的进价降低了4%,但售价未变,从而使童装店销售这种童鞋的利润提高了5%.这种童鞋原来每双进价是多少元?
(利润=售价-进价,利润率= )若设这种童鞋原来每双进价是x元,根据题意,可列方程为 .
三、解答题
-
19. 先化简,再求值:
,其中
20. 解方程:21. 平面内有四个点A,B,C,D,用它们作顶点可以组成几个三角形?画出图形,并写出存在的三角形.(只写含已知字母的)22. 利用多项式的乘法法则可以推导得出:=
=
型式子是数学学习中常见的一类多项式,因式分解是与整式乘法方向相反的变形,利用这种关系可得
①
因此,利用①式可以将 型式子分解因式.
例如:将式子 分解因式,这个式子的二次项系数是1,常数项 ,一次项系数 ,因此利用①式可得 .
上述分解因式 的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(图1)
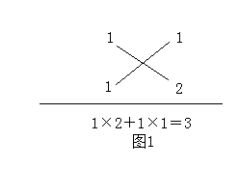
这样,我们也可以得到 .
这种方法就是因式分解的方法之一 十字相乘法.
(1)、利用这种方法,将下列多项式分解因式:(2)、