河北省承德市承德县2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-11-13 类型:期末考试
一、单选题
-
1. 下列各数中,其相反数等于本身的是( )A、﹣1 B、0 C、1 D、20182. 下列各组整式中是同类项的是( )A、 与 B、 与 C、 与 D、 与3. 已知x=y , 则下面变形错误的是( )A、x+a=y+a B、x-a=y-a C、2x=2y D、4. 下列说法正确的是( )A、﹣ 的系数是﹣2 B、x2+x﹣1的常数项为1 C、22ab3的次数是6次 D、2x﹣5x2+7是二次三项式5. 如图,某同学沿直线将三角形的一个角(阴影部分)剪掉后,发现剩下部分的周长比原三角形的周长小,能较好地解释这一现象的数学知识是( )
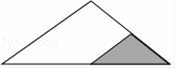 A、两点确定一条直线 B、线段是直线的一部分 C、经过一点有无数条直线 D、两点之间,线段最短6. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数,如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为( )
A、两点确定一条直线 B、线段是直线的一部分 C、经过一点有无数条直线 D、两点之间,线段最短6. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数,如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为( )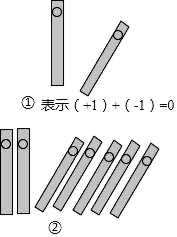 A、﹣1 B、﹣2 C、﹣3 D、﹣47. 用分配律计算 ,去括号后正确的是( )A、 B、 C、 D、8. 将一副三角尺按不同位置摆放,摆放方式中∠α 与∠β 互余的是( )A、
A、﹣1 B、﹣2 C、﹣3 D、﹣47. 用分配律计算 ,去括号后正确的是( )A、 B、 C、 D、8. 将一副三角尺按不同位置摆放,摆放方式中∠α 与∠β 互余的是( )A、 B、
B、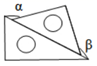 C、
C、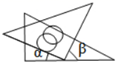 D、
D、 9. 在解方程 时,去分母正确的是( )A、 B、 C、 D、10. A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车速度为120千米/小时,乙车速度为80千米/小时,经过t小时两车相距50千米.则t的值是( )A、2 B、2或2.25 C、2.5 D、2或2.511. 下列各式中,不相等的是( )A、 和 B、 和 C、 和 D、 和12. 如图,射线OA的端点O在直线CD上,若∠COA=37°,则∠AOD的度数是( )
9. 在解方程 时,去分母正确的是( )A、 B、 C、 D、10. A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车速度为120千米/小时,乙车速度为80千米/小时,经过t小时两车相距50千米.则t的值是( )A、2 B、2或2.25 C、2.5 D、2或2.511. 下列各式中,不相等的是( )A、 和 B、 和 C、 和 D、 和12. 如图,射线OA的端点O在直线CD上,若∠COA=37°,则∠AOD的度数是( ) A、163° B、143° C、167° D、148°13. 如图,一个窗户的上部分是由4个相同的扇形组成的半圆,下部分是由边长为 的4个完全相同的小正方形组成的长方形,则做出这个窗户需要的材料总长是( )
A、163° B、143° C、167° D、148°13. 如图,一个窗户的上部分是由4个相同的扇形组成的半圆,下部分是由边长为 的4个完全相同的小正方形组成的长方形,则做出这个窗户需要的材料总长是( ) A、 B、 C、 D、14. 下列结论正确的是( )
A、 B、 C、 D、14. 下列结论正确的是( )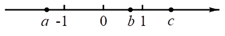 A、c>a>b B、 > C、|a|<|b| D、abc>015. 已知x2+3x+5的值是7,则式子﹣3x2﹣9x+2的值是( )A、0 B、﹣2 C、﹣4 D、﹣616. 我们知道,无限循环小数都可以转化为分数.例如:将 转化为分数时,可设 ,则 ,解得 ,即 .仿照这种方法,将 化成分数是( )A、 B、 C、 D、
A、c>a>b B、 > C、|a|<|b| D、abc>015. 已知x2+3x+5的值是7,则式子﹣3x2﹣9x+2的值是( )A、0 B、﹣2 C、﹣4 D、﹣616. 我们知道,无限循环小数都可以转化为分数.例如:将 转化为分数时,可设 ,则 ,解得 ,即 .仿照这种方法,将 化成分数是( )A、 B、 C、 D、二、填空题
-
17. 计算: .18. 已知 为非零有理数,当 时, ;当 时, .19. 用火柴棍按图所示的方式摆大小不同的“F”,第1个“F”需要4根,第2个需要7根,第3个需要10根,依此规律,第6个需要根,第n个需要根(用 含 n的代数式表示).

三、解答题
-
20. 计算:(1)、5﹣(﹣8);(2)、﹣22+3×(﹣1)2018﹣9÷(﹣3).21. 解方程:(1)、 ;(2)、 .22. 有一个水库某天8:00的水位为 (以警戒线为基准,记高于警戒线的水位为正),在以后的6个时刻测得的水位升降情况如下(记上升为正,单位: ): .经这6次水位升降后,水库的水位超过警戒线了吗?23. 如图所示,一块正方形纸板剪去四个相同的三角形后留下了阴影部分的图形.已知正方形的边长为a,三角形的高为h.
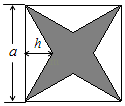 (1)、用式子表示阴影部分的面积(2)、当a=2,h= 时,求阴影部分的面积.24. 已知A=2a2+3ab﹣2a﹣1,B=﹣a2+(1)、当a=﹣1,b=﹣2时,求4A﹣(3A﹣2B)的值;(2)、若(1)中式子的值与a的取值无关,求b的值.25. 定义:若关于x的一元一次方程ax=b的解为b+a , 则称该方程为“和解方程”,例如:2x=﹣4的解为x=﹣2,且﹣2=﹣4+2,则该方程2x=﹣4是和解方程.(1)、判断﹣3x= 是否是和解方程,说明理由;(2)、若关于x的一元一次方程5x=m﹣2是和解方程,求m的值.26. 如果两个角的差的绝对值等于 ,就称这两个角互为反余角,其中一个角叫做另一个角的反余角,例如, , , ,则 和 互为反余角,其中 是 的反余角, 也是 的反余角.
(1)、用式子表示阴影部分的面积(2)、当a=2,h= 时,求阴影部分的面积.24. 已知A=2a2+3ab﹣2a﹣1,B=﹣a2+(1)、当a=﹣1,b=﹣2时,求4A﹣(3A﹣2B)的值;(2)、若(1)中式子的值与a的取值无关,求b的值.25. 定义:若关于x的一元一次方程ax=b的解为b+a , 则称该方程为“和解方程”,例如:2x=﹣4的解为x=﹣2,且﹣2=﹣4+2,则该方程2x=﹣4是和解方程.(1)、判断﹣3x= 是否是和解方程,说明理由;(2)、若关于x的一元一次方程5x=m﹣2是和解方程,求m的值.26. 如果两个角的差的绝对值等于 ,就称这两个角互为反余角,其中一个角叫做另一个角的反余角,例如, , , ,则 和 互为反余角,其中 是 的反余角, 也是 的反余角.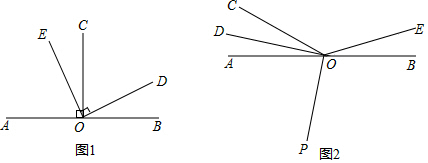 (1)、如图 为直线AB上一点, 于点O, 于点O,则 的反余角是 , 的反余角是;(2)、若一个角的反余角等于它的补角的 ,求这个角.(3)、如图2,O为直线AB上一点, ,将 绕着点O以每秒 角的速度逆时针旋转得 ,同时射线OP从射线OA的位置出发绕点O以每秒 角的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒,求当t为何值时, 与 互为反余角 图中所指的角均为小于平角的角 .
(1)、如图 为直线AB上一点, 于点O, 于点O,则 的反余角是 , 的反余角是;(2)、若一个角的反余角等于它的补角的 ,求这个角.(3)、如图2,O为直线AB上一点, ,将 绕着点O以每秒 角的速度逆时针旋转得 ,同时射线OP从射线OA的位置出发绕点O以每秒 角的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒,求当t为何值时, 与 互为反余角 图中所指的角均为小于平角的角 .