河北省保定市高阳县2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-11-13 类型:期末考试
一、单选题
-
1. 下列各式的最小值是( )A、1-3 B、 C、 D、2. 环境污染刻不容缓,据统计全球每分钟约有8521000吨污水排出,把8521000用科学记数法表示( )A、 B、 C、 D、3. 如图,数轴上有A,B,C,D四个点,其中表示互为倒数的点是( )
 A、点A与点B B、点A与点D C、点B与点D D、点B与点C4. 下列各组式子中,是同类项的是( )A、3x2y与﹣3xy2 B、3xy与﹣2yx C、2x与2x2 D、5xy与5yz5. 如图是某几何体从不同角度看到的图形,这个几何体是( )
A、点A与点B B、点A与点D C、点B与点D D、点B与点C4. 下列各组式子中,是同类项的是( )A、3x2y与﹣3xy2 B、3xy与﹣2yx C、2x与2x2 D、5xy与5yz5. 如图是某几何体从不同角度看到的图形,这个几何体是( )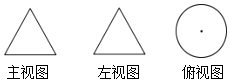 A、圆锥 B、圆柱 C、正三棱柱 D、三棱锥6. 一个正方体的六个面上分别标有-1,-2,-3,-4,-5,-6中的一个数,各个面上所标数字都不相同,如图是这个正方体的三种放置方法,则数字-3对面的数字是( )
A、圆锥 B、圆柱 C、正三棱柱 D、三棱锥6. 一个正方体的六个面上分别标有-1,-2,-3,-4,-5,-6中的一个数,各个面上所标数字都不相同,如图是这个正方体的三种放置方法,则数字-3对面的数字是( )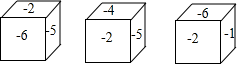 A、-1 B、-2 C、-5 D、-67. 当 分别等于1和 时,代数式 的两个值( )A、互为相反数 B、相等 C、互为倒数 D、异号8. 如图,C为线段AB上一点,D为线段BC的中点,AB=20,AD=14,则AC的长为( )
A、-1 B、-2 C、-5 D、-67. 当 分别等于1和 时,代数式 的两个值( )A、互为相反数 B、相等 C、互为倒数 D、异号8. 如图,C为线段AB上一点,D为线段BC的中点,AB=20,AD=14,则AC的长为( )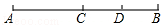 A、10 B、8 C、7 D、69. 已知 ,则式子 的值为( )A、4 B、 C、12 D、无法确定10. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有 辆车,则可列方程( )A、 B、 C、 D、11. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、
A、10 B、8 C、7 D、69. 已知 ,则式子 的值为( )A、4 B、 C、12 D、无法确定10. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有 辆车,则可列方程( )A、 B、 C、 D、11. 将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是( )A、 B、
B、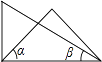 C、
C、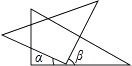 D、
D、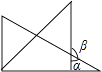 12. 如图,数轴表示的是5个城市的国际标准时间(单位:时),如果北京的时间是2020年1月9日上午9时,下列说法正确的是( )
12. 如图,数轴表示的是5个城市的国际标准时间(单位:时),如果北京的时间是2020年1月9日上午9时,下列说法正确的是( ) A、伦敦的时间是2020年1月9日凌晨1时 B、纽约的时间是2020年1月9日晚上20时 C、多伦多的时间是2020年1月8日晚上19时 D、汉城的时间是2020年1月9日上午8时13. 利用运算律简便计算52×(–999)+49×(–999)+999正确的是( )A、–999×(52+49)=–999×101=–100899 B、–999×(52+49–1)=–999×100=–99900 C、–999×(52+49+1)=–999×102=–101898 D、–999×(52+49–99)=–999×2=–199814. 如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )
A、伦敦的时间是2020年1月9日凌晨1时 B、纽约的时间是2020年1月9日晚上20时 C、多伦多的时间是2020年1月8日晚上19时 D、汉城的时间是2020年1月9日上午8时13. 利用运算律简便计算52×(–999)+49×(–999)+999正确的是( )A、–999×(52+49)=–999×101=–100899 B、–999×(52+49–1)=–999×100=–99900 C、–999×(52+49+1)=–999×102=–101898 D、–999×(52+49–99)=–999×2=–199814. 如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )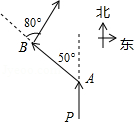 A、北偏东30° B、北偏东80° C、北偏西30° D、北偏西50°15. 多项式 的值随着 的取值不同而不同,下表是当 取不同值时对应的多项式的值,则关于 的方程 的解为( )
A、北偏东30° B、北偏东80° C、北偏西30° D、北偏西50°15. 多项式 的值随着 的取值不同而不同,下表是当 取不同值时对应的多项式的值,则关于 的方程 的解为( )0
1
2
4
0
A、 B、 C、0 D、无法确定16. 一列数 ,其中 ,则 ( )A、23 B、 C、24 D、二、填空题
-
17. 比较大小: (填“ ”“ ”“ ”)18. 已知 ,则 的补角为;19. 如图,约定上方相邻两数之和等于这两个数下方箭头共同指向的数:
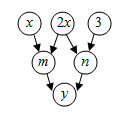 .
.示例:

即 ,则 ;
20. A、B两个动点在数轴上做匀速运动,它们的运动时间以及位置记录如表:时间(秒)
0
5
7
A点位置
19
﹣1
b
B点位置
a
17
27
A、B两点相距9个单位长度时,时间t的值为.
三、解答题
-
21. 计算:(1)、(2)、(3)、计算: ,直接写出下式的结果: .22. 计算:(1)、(2)、23. 计算:老师所留的作业中有这样一道题,解方程: 甲、乙两位同学完成的过程如下:

老师发现这两位同学的解答都有不符合题意.
(1)、甲同学的解答从第步开始出现不符合题意;错误的原因是;乙同学的解答从第步开始出现不符合题意,错误的原因是;(2)、请重新写出完成此题的符合题意解答过程.24. 已知(1)、计算 的值;(2)、计算 ;(3)、猜想 . (直接写出结果即可)25. 小马虎做一道数学题,“已知两个多项式 , ,试求 .”其中多项式 的二次项系数印刷不清楚.(1)、小马虎看答案以后知道 ,请你替小马虎求出系数“ ”;(2)、在(1)的基础上,小马虎已经将多项式 符合题意求出,老师又给出了一个多项式 ,要求小马虎求出 的结果.小马虎在求解时,误把“ ”看成“ ”,结果求出的答案为 .请你替小马虎求出“ ”的符合题意答案.26. 某商场春节促销活动出售 两种商品,活动方案如下两种:方案一
每件标价
90元
100元
每件商品返利
按标价的
按标价的
例如买一件 商品,只需付款 元
方案二
所购商品一律按标价20%的返利
(1)、某单位购买 商品 件, 商品20件,选用何种方案划算?(2)、某单位购买 商品件( 为正整数),购买 商品的件数是商品件数的2倍多1件。则两种方案的实际付款各多少?(3)、若两种方案的实际付款一样,求 的值.27. 分类讨论是一种非常重要的数学方法,如果一道题提供的已知条件中包含几种情况,我们可以分情况讨论来求解.例如:若|x|=2,|y|=3求x+y的值.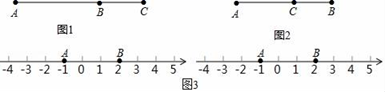
情况①若x=2,y=3时,x+y=5
情况②若x=2,y=﹣3时,x+y=﹣1
情况③若x=﹣2,y=3时,x+y=1
情况④若x=﹣2,y=﹣3时,x+y=﹣5
所以,x+y的值为1,﹣1,5,﹣5.
几何的学习过程中也有类似的情况:
(1)、问题(1):已知点A,B,C在一条直线上,若AB=8,BC=3,则AC长为多少?通过分析我们发现,满足题意的情况有两种
情况①当点C在点B的右侧时,如图1,此时,AC=
情况②当点C在点B的左侧时,如图2,此时,AC=
通过以上问题,我们发现,借助画图可以帮助我们更好的进行分类.
(2)、问题(2):如图3,数轴上点A和点B表示的数分别是﹣1和2,点C是数轴上一点,且BC=2AB,则点C表示的数是多少?仿照问题1,画出图形,结合图形写出分类方法和结果.
(3)、问题(3):点O是直线AB上一点,以O为端点作射线OC、OD,使∠AOC=60°,OCOD,求∠BOD的度数.画出图形,直接写出结果.