北京市通州区2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-11-13 类型:期末考试
一、单选题
-
1. 如图,从直线 外一点 向 引四条线段 , , , ,其中最短的一条是( )
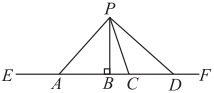 A、 B、 C、 D、2. 下列运算正确的是( ) .A、 B、 C、 D、3. 射线 , , , 的位置如图所示,可以读出 的度数为( )
A、 B、 C、 D、2. 下列运算正确的是( ) .A、 B、 C、 D、3. 射线 , , , 的位置如图所示,可以读出 的度数为( ) A、 B、 C、 D、4. 下面的几何体中,主(正)视图为三角形的是( )A、
A、 B、 C、 D、4. 下面的几何体中,主(正)视图为三角形的是( )A、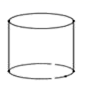 B、
B、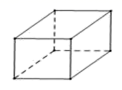 C、
C、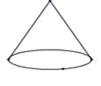 D、
D、 5. 下列各单项式中,与 是同类项的是( )A、 B、 C、 D、6. 已知 、 、 三个数在数轴上对应的点如图所示,下列结论错误的是( )
5. 下列各单项式中,与 是同类项的是( )A、 B、 C、 D、6. 已知 、 、 三个数在数轴上对应的点如图所示,下列结论错误的是( )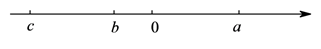 A、 B、 C、 D、7. 若OC是∠AOB内部的一条射线,则下列式子中,不能表示“OC是∠AOB的平分线”的是( )A、∠AOC=∠BOC B、∠AOB=2∠BOC C、∠AOC= ∠AOB D、∠AOC+∠BOC=∠AOB8. 按如图所示的运算程序,能使运算输出的结果为2的是( )
A、 B、 C、 D、7. 若OC是∠AOB内部的一条射线,则下列式子中,不能表示“OC是∠AOB的平分线”的是( )A、∠AOC=∠BOC B、∠AOB=2∠BOC C、∠AOC= ∠AOB D、∠AOC+∠BOC=∠AOB8. 按如图所示的运算程序,能使运算输出的结果为2的是( ) A、 , B、 , C、 , D、 ,9. 中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是,有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天整才到达目的地.求此人第六天走的路程为多少里,如果设此人第六天走的路程为 里,依题意,可列方程为( )A、 B、 C、 D、10. 对于两个不相等的有理数 , ,我们规定符号 表示 , 两数中较大的数,例如 .按照这个规定,那么方程 的解为( )A、-1 B、 C、1 D、-1或
A、 , B、 , C、 , D、 ,9. 中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是,有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天整才到达目的地.求此人第六天走的路程为多少里,如果设此人第六天走的路程为 里,依题意,可列方程为( )A、 B、 C、 D、10. 对于两个不相等的有理数 , ,我们规定符号 表示 , 两数中较大的数,例如 .按照这个规定,那么方程 的解为( )A、-1 B、 C、1 D、-1或二、填空题
-
11. 计算 的结果是.12. 如果关于x的方程 的解是x=2,那么m的值是.13. 绝对值大于1.5并且小于3的整数是.14. 把 换算成度,结果是.15. 某正方体每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“我”字所在面相对的面上的汉字是.
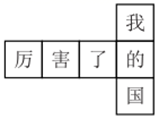 16. 已知点 在线段 上,再添加一个条件才能说明点 是线段 的中点,那么这个条件可以是.17. 写出一个系数为负数且次数为4的单项式,并要求此单项式中所含字母只有m,n.18. 已知 , ,且 , ,那么 的值为.19. 已知 ,以点 为端点作射线 ,使 ,再作 的平分线 ,那么 的度数为.20. 我们知道,无限循环小数都可以转化为分数.例如:将 转化为分数时,可设 ,则 , , ,解得 ,即 .仿此方法,将 化成分数是 , 将 化成分数是.
16. 已知点 在线段 上,再添加一个条件才能说明点 是线段 的中点,那么这个条件可以是.17. 写出一个系数为负数且次数为4的单项式,并要求此单项式中所含字母只有m,n.18. 已知 , ,且 , ,那么 的值为.19. 已知 ,以点 为端点作射线 ,使 ,再作 的平分线 ,那么 的度数为.20. 我们知道,无限循环小数都可以转化为分数.例如:将 转化为分数时,可设 ,则 , , ,解得 ,即 .仿此方法,将 化成分数是 , 将 化成分数是.三、解答题
-
21. 计算:(1)、 ;(2)、 .22. 先化简再求值:(1)、 ,其中 , ;(2)、 ,其中 .23. 解下列方程:(1)、 ;(2)、 .24. 已知线段 ,点 在射线 上,且 ,点 是 的中点,依题意画出图形并求线段 的长.25. 数学课上,某班同学用天平和一些物品(如图)探究了等式的基本性质.该班科技创新小组的同学提出问题:仅用一架天平和一个10克的砝码能否测量出乒乓球和一次性纸杯的质量?科技创新小组的同学找来足够多的乒乓球和某种一次性纸杯(假设每个乒乓球的质量相同,每个纸杯的质量也相同),经过多次试验得到以下记录:

记录
天平左边
天平右边
状态
记录一
6个乒乓球,
1个10克的砝码
14个一次性纸杯
平衡
记录二
8个乒乓球
7个一次性纸杯,
1个10克的砝码
平衡
请算一算,一个乒乓球的质量是多少克?一个这种一次性纸杯的质量是多少克?
解:
(1)、设一个乒乓球的质量是 克,则一个这种一次性纸杯的质量是克;(用含 的代数式表示)(2)、列一元一次方程求一个乒乓球的质量,并求出一个这种一次性纸杯的质量.26. 如图,以直线 上一点 为端点作射线 ,使 ,在同一个平面内将一个直角三角板的直角顶点放在点 处.(注: )(1)、如图1,如果直角三角板 的一边 放在射线 上,那么 的度数为;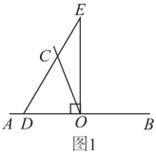 (2)、如图2,将直角三角板 绕点 按顺时针方向转动到某个位置,如果 恰好平分 ,求 的度数;
(2)、如图2,将直角三角板 绕点 按顺时针方向转动到某个位置,如果 恰好平分 ,求 的度数;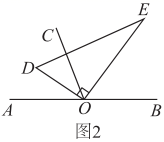 (3)、如图3,将直角三角板 绕点 任意转动,如果 始终在 的内部,请直接用等式表示 和 之间的数量关系.
(3)、如图3,将直角三角板 绕点 任意转动,如果 始终在 的内部,请直接用等式表示 和 之间的数量关系.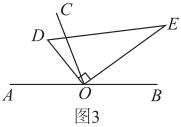 27. 在数轴上,我们把表示数2的点定为核点,记作点 ,对于两个不同的点 和 ,若点 , 到点 的距离相等,则称点 与点 互为核等距点.如图,点 表示数-1,点 表示数5,它们与核点 的距离都是3个单位长度,我们称点 与点 互为核等距点.
27. 在数轴上,我们把表示数2的点定为核点,记作点 ,对于两个不同的点 和 ,若点 , 到点 的距离相等,则称点 与点 互为核等距点.如图,点 表示数-1,点 表示数5,它们与核点 的距离都是3个单位长度,我们称点 与点 互为核等距点.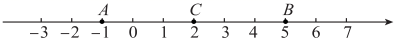 (1)、已知点 表示数3,如果点 与点 互为核等距点,那么点 表示的数是;(2)、已知点 表示数 ,点 与点 互为核等距点,
(1)、已知点 表示数3,如果点 与点 互为核等距点,那么点 表示的数是;(2)、已知点 表示数 ,点 与点 互为核等距点,①如果点 表示数 ,求 的值;
②对点 进行如下操作:先把点 表示的数乘以2,再把所得数表示的点沿着数轴向左移动5个单位长度得到点 ,求 的值.
28. 我们把按一定规律排列的一列数称为数列,若对于一个数列中任意相邻有序的三个数 , , ,总满足 ,则称这个数列为理想数列.(1)、在数列① , , , ;②3,-2,-1,1中,是理想数列的是(只填序号即可)(2)、如果数列 ,是理想数列,求 的值;(3)、若数列 ,是理想数列,求代数式 的值;(4)、请写出一个由五个不同正整数组成的理想数列:.