北京市怀柔区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-13 类型：期末考试

进入出卷网下载

一、单选题

1. 4的相反数是（）.

A、4 B、-4 C、 $\frac{1}{4}$ D、-（-4）

查看试题解析
2. 如图所示的圆柱体从正面看得到的图形可能是（）

A、 B、 C、 D、

查看试题解析
3. 怀柔某天的最高气温是 $7 ° C$ ，最低气温是 $- 1 ° C$ ，则这天的温差是（）

A、 $- 8 ° C$ B、 $- 6 ° C$ C、 $6 ° C$ D、 $8 ° C$

查看试题解析
4. 一个几何体的展开图如图所示，这个几何体是（）

A、三棱柱 B、三棱锥 C、四棱柱 D、四棱锥

查看试题解析
5. 如图，点P在直线l外，点A，B在直线l上，PA=3，PB=7，点P到直线l的距离可能是（）

A、2 B、4 C、7 D、8

查看试题解析
6. 下列运算正确的是（）

A、 $4 m - m = 3$ B、 $a^{2} - a^{2} = a$ C、 $2 x y - y x = x y$ D、 $a^{2} b - a b^{2} = 0$

查看试题解析
7. 2019年10月1日，天安门广场有200000军民参加盛大的阅兵仪式和群众游行，欢庆伟大祖国70周年华诞.把200000用科学记数法表示为（）

A、 $2 \times 10^{3}$ B、 $2 \times 10^{4}$ C、 $2 \times 10^{5}$ D、 $2 \times 10^{6}$

查看试题解析
8. 有理数a，b在数轴上的对应点的位置如图所示，则下列各式成立的是（）

A、 $a > b$ B、 $a b > 0$ C、 $| a | < | b |$ D、 $- a > b$

查看试题解析
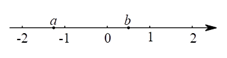9. 将一张长方形纸条折成如图所示的形状，BC为折痕.若∠DBA＝70°，则∠ABC等于（）

A、45° B、55° C、70° D、110°

查看试题解析
10. 如图，表中给出的是某月的月历，任意选取“U”型框中的7个数（如阴影部分所示），请你运用所学的数学知识来研究，发现这7个数的和不可能的是（）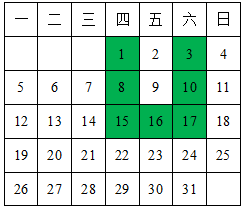

A、70 B、78 C、84 D、 $105$

查看试题解析

二、填空题

11. 写出一个比 $- 2 \frac{3}{4}$ 小的有理数：.

查看试题解析
12. 单项式 $- \frac{1}{3} x^{2} y^{3}$ 的系数是，次数是.

查看试题解析
13. 若 $| x | = 3$ ，则x= ．

查看试题解析
14. 若a,b互为相反数，则 $2 a + 2 b$ 的值为.

查看试题解析
15. 若 $∠ α = 47 ° 30'$ ，则90°- $∠ α$ 等于.

查看试题解析
16. 若是关于x的一元一次方程ax=x-2的解为x=2，则a= .

查看试题解析
17. 如图是一个正方形，把此正方形沿虚线AB减去一个角，得到一个五边形，则这个五边形的周长原来正方形的周长.（填“大于”“小于”或“等于”），理由是

查看试题解析
18. 我国古代《洛书》古称龟书，传说有神龟出于洛水，其甲壳上记载着一个世界上最古老的的幻方，如图所示，若将1~9这九个数字填入这个3×3的幻方中，恰好能使三行、三列、对角的三个数字之和分别相等.根据题意，要求幻方中的m则可列方程为，进而可求得m= ， n=.

查看试题解析

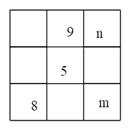
三、解答题

19. 计算： $- 6 - (- 13) + (- 9)$ .

查看试题解析
20. 计算： $- 8 \times (\frac{1}{8} + \frac{1}{4} - \frac{3}{2})$

查看试题解析
21. 计算： ${(- 1)}^{2020} + | - \frac{1}{2} | \div (- 4) \times 8$ .

查看试题解析
22. 解方程： $4 x + 2 (5 - x) = 6$ .

查看试题解析
23. $\frac{4 x - 1}{6} = 1 - \frac{3 x - 1}{3}$

查看试题解析
24. 如图，已知A，B，C，D四点，按要求画图：

(1)、画线段AB，射线AD，直线AC；

(2)、连结点B，D与直线AC交于点E；

(3)、连结点B，C，并延长线段BC与射线AD交于点O；

(4)、用量角器测量 $∠ A O B$ 的大小（精确到度）.

查看试题解析
25. 如图， $∠ C A B + ∠ A B C = 86 °$ ， $A D$ 平分 $∠ C A B$ ，与 $B C$ 边交于点 $D$ ， $B E$ 平分 $∠ A B C$ ，与 $A C$ 边交于点 $E$ .

(1)、依题意补全图形，并猜想 $∠ D A B + ∠ E B A$ 的度数等于；

(2)、填空，补全下面的证明过程.
∵ $A D$ 平分 $∠ C A B$ ， $B E$ 平分 $∠ A B C$ ，

∴ $∠ D A B = \frac{1}{2} ∠ C A B$ ， $∠ E B A = \underline{}$ .（理由： ▲ ）

∵ $∠ C A B + ∠ A B C = 86 °$ ，

∴ $∠ D A B + ∠ E B A =$ ▲ $\times (∠$ ▲ $+ ∠$ ▲ $) =$ ▲ $°$ .

查看试题解析
26. 在把下图折叠成正方体后，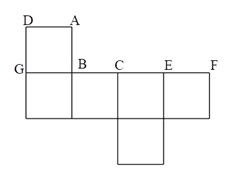

(1)、AB与GB的位置关系是；

(2)、CB与GB的位置关系是；

(3)、AB与BC的位置关系是，理由解释为.

查看试题解析
27. 把一些图书分给某班学生阅读，如果每人分3本，则剩余10本，如果每人分4本，则缺20本，问这个班有多少学生.

查看试题解析
28. 某校初一年级两个班的学生要到航天科普教育基地进行社会大课堂活动，其中初一（1）班有40多人，初一（2）班有50多人，教育基地门票价格如下：

原计划两班都以班为单位分别购票，则一共应付1106元.请回答下列问题：

(1)、初一（2）班有多少人？

(2)、你作为组织者如何购票最省钱？比原计划省多少钱？

查看试题解析
29. 根据下图回答问题：

(1)、已知∠ABC=90°，∠CBD=30°，BP平分∠ABD，请补全图形，并求∠ABP的度数.

(2)、在（1）的条件下，若∠ABC=α，∠CBD=β，直接写出∠ABP的度数.

查看试题解析
30. 阅读下面一段文字：
在数轴上点A，B分别表示数a，b.A，B两点间的距离可以用符号 $| A B |$ 表示，利用有理数减法和绝对值可以计算A，B两点之间的距离 $| A B |$ .
例如：当a=2，b=5时， $| A B |$ =5-2=3；当a=2，b=-5时， $| A B |$ = $| - 5 - 2 |$ =7；当a=-2，b=-5时， $| A B |$ = $| - 5 - (- 2) |$ =3.综合上述过程，发现点A、B之间的距离 $| A B |$ = $| b - a |$ (也可以表示为 $| a - b |$ ).
请你根据上述材料，探究回答下列问题：

(1)、数轴上表示1和3两点之间的距离是；

(2)、表示数a和-2的两点间距离是6，则a=；

(3)、如果数轴上表示数a的点位于-4和3之间，求 $| a + 4 | + | a - 3 |$ 的值.

(4)、是否存在数a，使代数式 $| a - 1 | + | a - 2 | + | a - 3 |$ 的值最小？若存在，请求出代数式的最小值，并直接写出数a的值或取值范围，若不存在，请简要说明理由.

查看试题解析