北京市海淀区2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-11-13 类型:期末考试
一、单选题
-
1. “ ”字手势表达胜利,必胜的意义.它源自于英国,“ ”为英文 (胜利)的首字母.现在“V"字手势早已成为世界用语了.如图的“ ”字手势中,食指和中指所夹锐角 的度数为( )
 A、 B、 C、 D、2. 2019年10月1日国庆阅兵是中国特色社会主义进入新时代的首次阅兵,也是人民军队改革重塑后的首次集中亮相.此次阅兵编 个方(梯)队和联合军团,总规模约 万人将“ 万”用科学记数法表示应为( )A、 B、 C、 D、3. 下表是11月份某一天北京四个区的平均气温:
A、 B、 C、 D、2. 2019年10月1日国庆阅兵是中国特色社会主义进入新时代的首次阅兵,也是人民军队改革重塑后的首次集中亮相.此次阅兵编 个方(梯)队和联合军团,总规模约 万人将“ 万”用科学记数法表示应为( )A、 B、 C、 D、3. 下表是11月份某一天北京四个区的平均气温:区县
海淀
怀柔
密云
昌平
气温
这四个区中该天平均气温最低的是( )
A、海淀 B、怀柔 C、密云 D、昌平4. 下列计算正确的是( )A、 B、 C、 D、5. 已知关于 的方程 的解是 ,则 的值为( )A、 B、 C、 D、6. 有理数 在数轴上的对应点的位置如图所示,则正确的结论是( ) A、 B、 C、 D、7. 下列等式变形正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则8. 北京大兴国际机场采用“三纵一横”全向型跑道构型,可节省飞机飞行时间,遇极端天气侧向跑道可提升机场运行能力.跑道的布局为:三条南北向的跑道和一条偏东南走向的侧向跑道.如图,侧向跑道AB在点O南偏东70°的方向上,则这条跑道所在射线OB与正北方向所成角的度数为( )
A、 B、 C、 D、7. 下列等式变形正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则8. 北京大兴国际机场采用“三纵一横”全向型跑道构型,可节省飞机飞行时间,遇极端天气侧向跑道可提升机场运行能力.跑道的布局为:三条南北向的跑道和一条偏东南走向的侧向跑道.如图,侧向跑道AB在点O南偏东70°的方向上,则这条跑道所在射线OB与正北方向所成角的度数为( )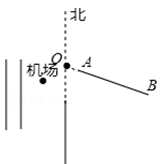 A、20° B、70° C、110° D、160°9. 已知线段 ,下面有四个说法: ①线段 长可能为 ;②线段 长可能为 ;③线段 长不可能为 ;④线段 长可能为 .所有正确说法的序号是( )A、①② B、③④ C、①②④ D、①②③④10. 某长方体的展开图中, (均为格点)的位置如图所示,一只蚂蚁从点 出发,沿着长方体表面爬行.若此蚂蚁分别沿最短路线爬行到 四点,则蚂蚁爬行距离最短的路线是( )
A、20° B、70° C、110° D、160°9. 已知线段 ,下面有四个说法: ①线段 长可能为 ;②线段 长可能为 ;③线段 长不可能为 ;④线段 长可能为 .所有正确说法的序号是( )A、①② B、③④ C、①②④ D、①②③④10. 某长方体的展开图中, (均为格点)的位置如图所示,一只蚂蚁从点 出发,沿着长方体表面爬行.若此蚂蚁分别沿最短路线爬行到 四点,则蚂蚁爬行距离最短的路线是( )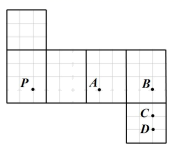 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 厂家检测甲、乙、丙、丁四个足球的质量,超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的足球是 .
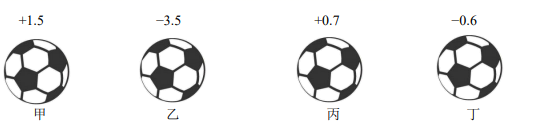 12. 一个单项式满足下列两个条件:①系数是﹣2;②次数是3.写出一个满足上述条件的单项式: .13. 计算,14. 如图,将五边形 沿虚线裁去一个角得到六边形 ,则该六边形的周长一定比原五边形的周长(填:大或小), 理由为.
12. 一个单项式满足下列两个条件:①系数是﹣2;②次数是3.写出一个满足上述条件的单项式: .13. 计算,14. 如图,将五边形 沿虚线裁去一个角得到六边形 ,则该六边形的周长一定比原五边形的周长(填:大或小), 理由为.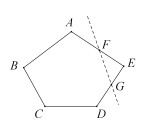 15. 已知一个长为 ,宽为 的长方形,如图1所示,沿图中虚线裁剪成四个相同的小长方形,按图2的方式拼接,则阴影部分正方形的边长是.(用含 的代数式表示)
15. 已知一个长为 ,宽为 的长方形,如图1所示,沿图中虚线裁剪成四个相同的小长方形,按图2的方式拼接,则阴影部分正方形的边长是.(用含 的代数式表示) 16. 如下图,点 在线段 上, 是线段 的中点.若 ,则线段 的长为 .
16. 如下图,点 在线段 上, 是线段 的中点.若 ,则线段 的长为 . 17. 历史上数学家欧拉最先把关于 的多项式用记号 来表示,把 等于某数 时的多项式的值用 来表示.例如,对于多项式 ,当 时,多项式的值为 ,若 ,则 的值为.18. 小明家想要从某场购买洗衣机和烘干机各一台,现在分别从 两个品牌中各选中一款洗衣机和一款烘干机,它们的单价如表1所示.目前该商场有促销活动,促销方案如表2所示.
17. 历史上数学家欧拉最先把关于 的多项式用记号 来表示,把 等于某数 时的多项式的值用 来表示.例如,对于多项式 ,当 时,多项式的值为 ,若 ,则 的值为.18. 小明家想要从某场购买洗衣机和烘干机各一台,现在分别从 两个品牌中各选中一款洗衣机和一款烘干机,它们的单价如表1所示.目前该商场有促销活动,促销方案如表2所示.
表2:商场促销方案
①所有商品均享受8折优惠.
②所有洗衣机均可享受节能减排补贴,补贴标准为:在折后价的基础t.
再减免13%。
③若同时购买同品牌洗 衣机和烘干机,额外可享受“满两件减400元"
则选择品种的洗衣机和品种的烘干机支付总费用最低,支付总费用最低为元.
三、解答题
-
19. 计算:(1)、(2)、20. 解方程:(1)、(2)、21. 先化简,再求值: ,其中 .22. 如图,已知平面上三点 ,请按要求完成下列问题:
 (1)、画射线 ,线段 ;(2)、连接 ,并用圆规在线段 的延长线上截取 ,连接 (保留画图痕迹);(3)、利用刻度尺取线段 的中点 ,连接 .23. 下图是一个运算程序:
(1)、画射线 ,线段 ;(2)、连接 ,并用圆规在线段 的延长线上截取 ,连接 (保留画图痕迹);(3)、利用刻度尺取线段 的中点 ,连接 .23. 下图是一个运算程序: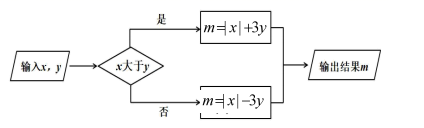 (1)、若 ,求 的值;(2)、若 ,输出结果 的值与输入 的值相同,求 的值.24. 2019年9月29日,中国女排以十一连胜的战绩夺得女排世界杯冠军,成为世界三大赛的“十冠王”2019 年女排世界杯的参赛队伍为 支,比赛采取单循环方式,五局三胜,积分规则如下:比赛中以 或者 取胜的球队积 分,负队积 分;而在比赛中以 取胜的球队积 分,负队积 分.前四名队伍积分榜部分信息如下表所示,
(1)、若 ,求 的值;(2)、若 ,输出结果 的值与输入 的值相同,求 的值.24. 2019年9月29日,中国女排以十一连胜的战绩夺得女排世界杯冠军,成为世界三大赛的“十冠王”2019 年女排世界杯的参赛队伍为 支,比赛采取单循环方式,五局三胜,积分规则如下:比赛中以 或者 取胜的球队积 分,负队积 分;而在比赛中以 取胜的球队积 分,负队积 分.前四名队伍积分榜部分信息如下表所示, (1)、中国队 场胜场中只有一场以 取胜,请将中国队的总积分填在表格中.(2)、巴西队积 分取胜的场次比积 分取胜的场次多 场,且负场积分为 分,总积分见下表,求巴西队胜场的场数.25. 在数轴上,四个不同的点 分别表示有理数 ,且 .(1)、如图1, 为线段 的中点,
(1)、中国队 场胜场中只有一场以 取胜,请将中国队的总积分填在表格中.(2)、巴西队积 分取胜的场次比积 分取胜的场次多 场,且负场积分为 分,总积分见下表,求巴西队胜场的场数.25. 在数轴上,四个不同的点 分别表示有理数 ,且 .(1)、如图1, 为线段 的中点,
当点 与原点 重合时,用等式表示 与 的关系为;
(2)、求点 表示的有理数 的值(用含 的代数式表示);(3)、已知 ,若三点 的位置如图所示,请在图中标出点 的位置;
 (4)、 的大小关系为(用“ ”连接)26. 阅读下面材料:小聪遇到这样一个问题: 如图1, ,请画一个 ,使 与 互补.
(4)、 的大小关系为(用“ ”连接)26. 阅读下面材料:小聪遇到这样一个问题: 如图1, ,请画一个 ,使 与 互补.
小聪是这样思考的:首先通过分析明确射线 在 的外部,画出示意图,如图2所示:然后通过构造平角找到 的补角 ,

如图3所示:进而分析要使 与 互补,则需 .

因此,小聪找到了解决问题的方法:反向延长射线 得到射线 ,利用量角器画出 的平分线 ,这样就得到了 与 互补
(1)、小聪根据自己的画法写出了已知和求证,请你完成证明.已知:如图3,点 在直线 上,射线 平分 .求证: 与 互补. . (2)、参考小聪的画法,请在下图中画出一个 ,使 与 互余.(保留画图痕迹)
(2)、参考小聪的画法,请在下图中画出一个 ,使 与 互余.(保留画图痕迹) (3)、已知 和 互余,射线 平分 ,射线 平分 .若 ,直接写出锐角 的度数是.27. 给定一个十进制下的自然数 ,对于 每个数位上的数,求出它除以 的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数 的“模二数”,记为 .如 .对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位.上的数分别相加,规定: 与 相加得 ; 与 相加得 与 相加得 ,并向左边一位进 .如 的“模二数” 相加的运算过程如下图所示.
(3)、已知 和 互余,射线 平分 ,射线 平分 .若 ,直接写出锐角 的度数是.27. 给定一个十进制下的自然数 ,对于 每个数位上的数,求出它除以 的余数,再把每一个余数按照原来的数位顺序排列,得到一个新的数,定义这个新数为原数 的“模二数”,记为 .如 .对于“模二数”的加法规定如下:将两数末位对齐,从右往左依次将相应数位.上的数分别相加,规定: 与 相加得 ; 与 相加得 与 相加得 ,并向左边一位进 .如 的“模二数” 相加的运算过程如下图所示.
根据以上材料,解决下列问题:
(1)、 的值为 , 的值为(2)、如果两个自然数的和的“模二数”与它们的“模二数”的和相等,则称这两个数“模二相加不变”.如 ,因为 ,所以 ,即 与 满足“模二相加不变”.①判断 这三个数中哪些与 “模二相加不变”,并说明理由;
(3)、②与 23 “模二相加不变”的两位数有个