北京市丰台区2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-11-13 类型:期末考试
一、单选题
-
1. 如图,下列生活物品中,从整体上看,形状是圆柱的是( )A、
 B、
B、 C、
C、 D、
D、 2. 是第五代移动通信技术, 网络理论下载速度可以达到每秒 以上,这意味着下载一部高清电影只需1秒.将1300000用科学记数法表示应为( )A、 B、 C、 D、3. 有理数 , 在数轴上的对应点的位置如图所示,则正确的结论是( )
2. 是第五代移动通信技术, 网络理论下载速度可以达到每秒 以上,这意味着下载一部高清电影只需1秒.将1300000用科学记数法表示应为( )A、 B、 C、 D、3. 有理数 , 在数轴上的对应点的位置如图所示,则正确的结论是( ) A、 B、 C、 D、4. 如果某天北京的最低气温为 ,中午12点的气温比最低气温高了 ,那么中午12点的气温为( )A、 B、 C、 D、5. 下列各组中的两项,属于同类项的是( )A、 与 B、 与 C、 与 D、 与6. 如果关于x的方程 的解集是 ,那么a的值是( )A、−2 B、−1 C、1 D、27. 如图,将一副三角尺按不同的位置摆放,下列各图中, 与 互余的是( )A、
A、 B、 C、 D、4. 如果某天北京的最低气温为 ,中午12点的气温比最低气温高了 ,那么中午12点的气温为( )A、 B、 C、 D、5. 下列各组中的两项,属于同类项的是( )A、 与 B、 与 C、 与 D、 与6. 如果关于x的方程 的解集是 ,那么a的值是( )A、−2 B、−1 C、1 D、27. 如图,将一副三角尺按不同的位置摆放,下列各图中, 与 互余的是( )A、 B、
B、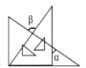 C、
C、 D、
D、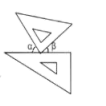 8. 如图,点 为线段 的中点,点 在线段 上,如果 , ,那么线段 的长是( )
8. 如图,点 为线段 的中点,点 在线段 上,如果 , ,那么线段 的长是( ) A、4 B、5 C、8 D、109. 在“ , , , , ”这5个算式中,运算结果为非负有理数的个数是( )A、5 B、4 C、3 D、210. 如图所示,直线 、 相交于点 ,“阿基米德曲线”从点 开始生成,如果将该曲线与每条射线的交点依次标记为2,-4,6,-8,10,-12,….那么标记为“-2020”的点在( )
A、4 B、5 C、8 D、109. 在“ , , , , ”这5个算式中,运算结果为非负有理数的个数是( )A、5 B、4 C、3 D、210. 如图所示,直线 、 相交于点 ,“阿基米德曲线”从点 开始生成,如果将该曲线与每条射线的交点依次标记为2,-4,6,-8,10,-12,….那么标记为“-2020”的点在( ) A、射线 上 B、射线 上 C、射线 上 D、射线 上
A、射线 上 B、射线 上 C、射线 上 D、射线 上二、填空题
-
11. 的相反数是 .12. 如图是某几何体的展开图,该几何体是.
 13. .14. 下图所示的网格是正方形网格, .(填“ ”,“ ”或“ ”)
13. .14. 下图所示的网格是正方形网格, .(填“ ”,“ ”或“ ”) 15. 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 .
15. 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 . 16. 下面的框图表示了琳琳同学解方程 的流程:
16. 下面的框图表示了琳琳同学解方程 的流程:
你认为琳琳同学在解这个方程的过程中从第步开始出现问题,符合题意完成这一步的依据是.
17. 的含义是:数轴上表示数 的点与原点的距离,那么 的含义是;如果 ,那么 的值是.18. 请你依据下面的情境,补充相应的条件和问题,使解决该实际问题的方程为 为了倡导同学们开展有益的课外活动,某校七年级组织了“爱我中国”合唱节评比活动.老师为参加比赛的5个班级都准备了一份奖品.三、解答题
-
19. 计算:20. 计算:(﹣12)×( + ).21. 计算:22. 解方程:23. 解方程:24. 先简化,再求值: ,其中 ,25. 下面是小明某次作图的过程,已知:如图,线段 , .

做法:①画射线 ;
②用圆规在射线 上截取一点 ,使线段 ;
③用圆规在射线 上截取一点 ,使线段 .
根据小明的作图过程,
(1)、补全所有符合小明作图过程的图形;(保留作图痕迹)(2)、线段 .(用含 , 的式子表示)26. 为了促进全民健身运动的开展,某市组织了一次足球比赛,下表记录了比赛过程中部分代表队的积分情况.代表队
场次(场)
胜(场)
平(场)
负(场)
积分(分)
6
5
1
0
16
6
6
0
0
18
6
3
2
1
11
6
3
1
2
10
(1)、本次比赛中,胜一场积分;(2)、参加此次比赛的 代表队完成10场比赛后,只输了一场,积分是23分,请你求出 代表队胜出的场数.27. 如图,货轮 在航行过程中,发现灯塔 在它北偏东 的方向上,同时,在它南偏西 、西北(即北偏西 )方向上又分别发现了客轮 和海岛 ,仿照表示灯塔方位的方法,画出表示客轮 和海岛 方向的射线. 28. 如图, 是直线 上一点, ,作射线 , ,使得 平分 , 平分 .求 的度数.
28. 如图, 是直线 上一点, ,作射线 , ,使得 平分 , 平分 .求 的度数. (1)、请依据题意补全图形;(2)、完成下面的解答过程:
(1)、请依据题意补全图形;(2)、完成下面的解答过程:解:因为 是直线 上一点,所以 .
由 ,得 ▲ °.
因为 平分 ,所以 ( ▲ ) ▲ °.
因为 平分 ,所以 ( ▲ ) ▲ °.
所以 ▲ °.
29. 小刚运用本学期的知识,设计了一个数学探究活动.如图1,数轴上的点 , 所表示的数分别为0,12.将一枚棋子放置在点 处,让这枚棋子沿数轴在线段 上往复运动(即棋子从点 出发沿数轴向右运动,当运动到点 处,随即沿数轴向左运动,当运动到点 处,随即沿数轴向右运动,如此反复⋯).并且规定棋子按照如下的步骤运动:第1步,从点 开始运动 个单位长度至点 处;第2步,从点 继续运动 单位长度至点 处;第3步,从点 继续运动 个单位长度至点 处…例如:当 时,点 、 、 的位置如图2所示.
解决如下问题:
(1)、如果 ,那么线段 ;(2)、如果 ,且点 表示的数为3,那么 ;(3)、如果 ,且线段 ,那么请你求出 的值.