北京市东城区2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-11-13 类型:期末考试
一、单选题
-
1. 5的相反数是( )A、 B、 C、 D、2. 北京大兴国际机场于2019年9月25日正式投入使用,新机场的运行将进一步满足北京地区的航空运输需求,增强国家民航竞争力,促进南北城区的均衡发展和京津冀协同发展.根据规划,2022年大兴国际机场客流量将达到4500万人次.4500用科学记数法表示为( )A、 B、 C、 D、3. 下列四个数中,最小的数是( )A、 B、 C、 D、4. 若 是关于 的方程 的解,则 的值为( )A、1 B、-1 C、7 D、-75. 下列计算正确的是( )A、 B、 C、 D、6. 把方程 去分母后,正确的是( ).A、 B、 C、 D、7. 如图是一副三角板摆成的图形,如果 ,那么 等于( )
 A、15° B、25° C、35° D、45°8. 下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程.其中可用基本事实 “两点之间,线段最短”来解释的现象有( )A、①② B、①③ C、②④ D、③④9. 实效m,n在数轴上的对应点如图所示,则下列各式子正确的是( )
A、15° B、25° C、35° D、45°8. 下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程.其中可用基本事实 “两点之间,线段最短”来解释的现象有( )A、①② B、①③ C、②④ D、③④9. 实效m,n在数轴上的对应点如图所示,则下列各式子正确的是( )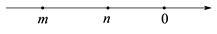 A、 B、 C、 D、10. 如图是某一立方体的侧面展开图,则该立方体是( )
A、 B、 C、 D、10. 如图是某一立方体的侧面展开图,则该立方体是( )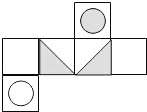 A、
A、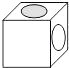 B、
B、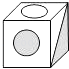 C、
C、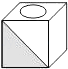 D、
D、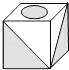
二、填空题
-
11. 某天最高气温为8℃,最低气温为﹣1℃,则这天的最高气温比最低气温高℃.12. 单项式 的次数是.13. 化简: .14. 写出一个能与 合并的单项式.15. 如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东60°的方向上,观测到小岛B在它南偏东38°的方向上,则∠AOB的度数是
 16. 《九章算术》是中国传统数学最重要的著作之一.书中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数几何?”意思是:“有若干人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:共有几个人?”设共有 个人共同出钱买鸡,根据题意,可列一元一次方程为.17. 已知线段 ,点D是线段AB的中点,直线AB上有一点C,并且 cm,则线段 .18. 观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2020个图形中共有 个.
16. 《九章算术》是中国传统数学最重要的著作之一.书中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数几何?”意思是:“有若干人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:共有几个人?”设共有 个人共同出钱买鸡,根据题意,可列一元一次方程为.17. 已知线段 ,点D是线段AB的中点,直线AB上有一点C,并且 cm,则线段 .18. 观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2020个图形中共有 个.
三、解答题
-
19. 计算:(1)、(2)、20. 解方程:(1)、(2)、21. 先化简,再求值: ,其中 , .22. 按照下列要求完成作图及问题解答:
如图,已知点A和线段BC.
 (1)、连接AB;(2)、作射线CA;(3)、延长BC至点D,使得BD=2BC;(4)、通过测量可得∠ACD的度数是(5)、画∠ACD的平分线CE.23. 一个角的余角比它的补角的还少40°,求这个角.24. 根据题意,补全解题过程:
(1)、连接AB;(2)、作射线CA;(3)、延长BC至点D,使得BD=2BC;(4)、通过测量可得∠ACD的度数是(5)、画∠ACD的平分线CE.23. 一个角的余角比它的补角的还少40°,求这个角.24. 根据题意,补全解题过程:如图,∠AOB=90°,OE平分∠AOC,OF平分∠BOC. 求∠EOF的度数.

解:因为OE平分∠AOC,OF平分∠BOC
所以∠EOC= ∠AOC,∠FOC= ▲ .
所以∠EOF=∠EOC- ▲
= (∠AOC- ▲ )
= ▲
= ▲ °.
25. 一般情况下,对于数 和 , (≠,不等号),但是对于某些特殊的数 和 , 我们把这些特殊的数 和 ,称为“理想数对”,记作 .例如当 时,有 ,那么 就是“理想数对”.(1)、 可以称为“理想数对”的是;(2)、如果 是“理想数对”,那么 =;(3)、若 是“理想数对”,求 的值.26. 为鼓励居民节约用电,某市试行每月阶梯电价收费制度,具体执行方案如下:档次
每户每月用电量(度)
执行电价(元/度)
第一档
小于或等于200
0.5
第二档
大于200且小于或等于450时,超出200的部分
0.7
第三档
大于450时,超出450的部分
1
(1)、一户居民七月份用电300度,则需缴电费元.(2)、某户居民五、六月份共用电500度,缴电费290元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于450度.①请判断该户居民五、六月份的用电量分别属于哪一个档次?并说明理由.
②求该户居民五、六月份分别用电多少度?
27. 已知 两点在数轴上所表示的数分别为 且满足 .(1)、则 , ;(2)、若点 从 点出发,以每秒1个单位长度的速度向右运动,同时点Q从M点出发,以每秒1个单位长度的速度向左运动,经过多长时间后 两点相距7个单位长度?(3)、若 为线段 上的两点,且 ,点 从点 出发,以每秒2个单位长度的速度向左运动,点 从 点出发,以每秒4个单位长度的速度向右运动,点R从B点出发,以每秒3个单位长度的速度向右运动,P,Q,R同时出发,是否存在常数 ,使得 的值与它们的运动时间无关,为定值。若存在,请求出 和这个定值;若不存在,请说明理由.