北京市大兴区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-13 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣3的相反数是（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、 $- 3$ D、 $3$

查看试题解析
2. 北京大兴国际机场航站楼形如展翅的凤凰，航站楼主体占地面积1030000平方米. 将1030000用科学记数法表示为（）

A、 $10.3 \times 10^{5}$ B、 $1.03 \times 10^{6}$ C、 $1.03 \times 10^{7}$ D、 $0.103 \times 10^{7}$

查看试题解析
3. 有理数 $a ， b$ 在数轴上的位置如图所示，则下列说法错误的是（）

A、 $a + b > 0$ B、 $b - a > 0$ C、 $a b < 0$ D、 $| a | > b$

查看试题解析
4. 方程 $- 3 x = \frac{1}{3}$ 的解是（）

A、 $x = - \frac{1}{9}$ B、 $x = - 9$ C、 $x = \frac{1}{9}$ D、 $x = 9$

查看试题解析
5. “比a的2倍大l的数”用代数式表示是（）

A、2（a+1） B、2（a﹣1） C、2a+1 D、2a﹣1

查看试题解析
6. 下列说法中正确的是（）

A、 $\frac{x + y}{2}$ 是单项式 B、 $\frac{1}{x}$ 是单项式 C、 $- \frac{2 x}{3}$ 的系数为-2 D、 $- 5 a^{2} b$ 的次数是3

查看试题解析
7. 下列四个图形中，不是正方体展开图的是（）

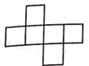A、 B、 C、 D、

查看试题解析
8. 已知下列四个应用题：①现有60个零件的加工任务，甲单独每小时可以加工4个零件，乙单独每小时可以加工6个零件.现甲乙两人合作，问两人开始工作几小时后还有20个零件没有加工？②甲乙两人从相距 $60 k m$ 的两地同时出发，相向面行，甲的速度是 $4 k m / h$ ，乙的速度是 $6 k m / h$ ，问经过几小时后两人相遇后又相距 $20 k m$ ？③甲乙两人从相距 $60 k m$ 的两地相向面行，甲的速度是 $4 k m / h$ ，乙的速度是 $6 k m / h$ ，如果甲先走了 $20 k m$ 后，乙再出发，问乙出发后几小时两人相遇？④甲乙两人从相距 $20 k m$ 的两地同时出发，背向而行，甲的速度是 $4 k m / h$ ，乙的速度是 $6 k m / h$ ，问经过几小时后两人相距 $60 k m$ ？其中，可以用方程 $4 x + 6 x + 20 = 60$ 表述题目中对应数量关系的应用题序号是（）

A、①②③④ B、①③④ C、②③④ D、①②

查看试题解析

二、填空题

9. 若 $- 2 a^{5} b$ 与 $a^{m + 2} b$ 是同类项，则 $m$ 的值是.

查看试题解析
10. 若|x－2|=3，则x的值是.

查看试题解析
11. 若代数式 $x - 2 y$ 的值是3，则代数式 $- 3 x + 6 y - 2$ 的值是.

查看试题解析
12. 请你写出一个含有常数项的二次二项式：．

查看试题解析
13. 11时整，钟表的时针与分针所构成锐角的度数是．

查看试题解析
14. 已知 $∠ α = 36 ° 15'$ ，则 $∠ α$ 的余角的度数．

查看试题解析
15. 用黑白两色的正方形纸片，按黑色纸片数逐渐加1的规律拼成一列图案：则第 $n$ 个图案中有白色纸片张．

查看试题解析
16. 对于有理数 $m$ ，我们规定 $[m]$ 表示不大于 $m$ 的最大整数，例如： $[1, 2] = 1$ ， $[3] = 3$ ， $[- 2.5] = - 3$ ，若 $[\frac{x + 2}{3}] = - 5$ ，则整数x的取值是．

查看试题解析

三、解答题

17. 计算： $(- 7) + 21 + (- 27) - 5$

查看试题解析
18. 计算： $- 4^{2} + 2 \times {(- 3)}^{2} - (- 6) \div (- \frac{4}{3})$

查看试题解析
19. 解方程： $2 (x - 1) - 5 = 7 x$

查看试题解析
20. 解方程： $\frac{x + 1}{2} - \frac{3 x - 1}{4} = 1$

查看试题解析
21. 先化简，再求值：
$2 (x^{2} y + x y) - (x^{2} y - x y) - 3 x^{2} y$ ，其中 $x = - 1$ ， $y = 1$ .

查看试题解析
22. 已知： $m^{2} + m n = 30$ ， $m n - n^{2} = - 10$ ，求下列代数式的值：

(1)、 $m^{2} + 2 m n - n^{2}$ ；

(2)、 $m^{2} + n^{2} - 7$ .

查看试题解析
23. 选择合适的画图工具，按要求作图并回答问题：
已知：如图点 $A$ ，点 $B$ ，点 $C$ ，

(1)、作直线 $A B$ ；

(2)、作线段 $A C$ ；

(3)、在点 $C$ 的东北方向有一点 $D$ ，且点 $D$ 在直线 $A B$ 上，画出点 $D$ ；

(4)、作射线 $C E$ 交 $A B$ 于点 $E$ ，使得 $∠ A C E = ∠ A$ ；

(5)、线段 $E A$ 与线段 $E C$ 的大小关系是.

查看试题解析
24. 列方程解应用题：
某学校组织初一年级学生参加公益劳动，在甲处劳动的有16人，在乙处劳动的有12人. 现在另调20人去甲乙两处支援，使得在甲处劳动的人数比在乙处劳动的人数的2倍少6人，问应调往甲、乙两处各多少人？

查看试题解析
25. 已知，一个角比它的补角的一半大 $15^{\circ}$ ，求这个角的度数.

查看试题解析
26. 已知，如图，点 $C$ 是线段 $A B$ 的中点，点 $D$ 是线段 $A C$ 的中点， $B C = 6 c m$ ，求线段 $B D$ 的长.

请将以下求解过程补充完整：

因为点 $C$ 是线段 $A B$ 的中点，

所以   ▲    ，

因为 $B C = 6 c m$ ，所以 $A C =$    ▲    $c m$ .

因为点 $D$ 是线段 $A C$ 的中点，

所以 $D C =$    ▲    .

所以 $D C =$    ▲    $c m$ .

所以 $B D =$    ▲    $=$    ▲    $c m$ .

查看试题解析
27. 如图， $O$ 为直线 $A B$ 上一点， $∠ A O C = 70^{\circ}$ ， $O D$ 是 $∠ A O C$ 的平分线， $∠ D O E = 90^{\circ}$ .

(1)、图中小于平角的角的个数是；

(2)、求 $∠ B O D$ 的度数；

(3)、猜想 $O E$ 是否平分 $∠ B O C$ ，并证明.

查看试题解析
28. 阅读材料并解决问题：

(1)、数学课上，老师提出如下问题：
观察下列算式：

$1^{2} - 0^{2} = 1 + 0 = 1$ ；

$2^{2} - 1^{2} = 2 + 1 = 3$ ；

$3^{2} - 2^{2} = 3 + 2 = 5$

$4^{2} - 3^{2} = 4 + 3 = 7$

$5^{2} - 4^{2} = 5 + 4 = 9$

…

若字母 $a ， b$ 表示自然数，用含 $a ， b$ 的式子表示观察得到的规律是 $a^{2} - b^{2} =$ ；

(2)、小云同学解决完老师提出的问题后，又继续研究，发现：
①当 $a ， b$ 表示负整数且 $a - b = 1$ 时，上述规律仍旧成立；

②当 $a ， b$ 表示分数且 $a - b = 1$ 时，上述规律仍旧成立.

请你对小云的两个发现进行验证，每个发现举出一个算式；

(3)、请你参照小云同学的研究思路，进行猜想，验证、归纳，当 $a - b = 2$ 时， $a^{2} - b^{2} =$ （用含 $a ， b$ 的代数式表示）；

(4)、进一步进行猜想、验证、归纳，当 $a - b = m$ （m为有理数）时， $a^{2} - b^{2} =$ （用含m，a，b的代数式表示）。

查看试题解析