北京市朝阳区2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-11-13 类型:期末考试
一、单选题
-
1. 2019年10月1日上午,庆祝中华人民共和国成立70周年大会在北京天安门广场隆重举行,超过200000军民以盛大的阅兵仪式和群众游行欢庆共和国70华诞.将200000用科学记数法表示为( )A、 B、 C、 D、2. 如图,数轴上有 , , , 四个点,所对应的数分别是 , , , ,下列各式的值最小的为( )
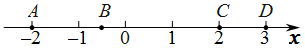 A、 B、 C、 D、3. 若 ,则 的补角的度数为( )A、 B、 C、 D、4. 明代数学家程大位的《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.”其大意为:有一群人分银子,如果每人分七两,则剩余四两,如果每人分九两,则还差半斤(注:明代时1斤=16两,故有“半斤八两”这个成语).设有 人分银子,根据题意所列方程正确的是( )A、 B、 C、 D、5. 如图,O为直线AB上一点,OM平分∠AOC , ON平分∠BOC , 则图中互余的角有( )
A、 B、 C、 D、3. 若 ,则 的补角的度数为( )A、 B、 C、 D、4. 明代数学家程大位的《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.”其大意为:有一群人分银子,如果每人分七两,则剩余四两,如果每人分九两,则还差半斤(注:明代时1斤=16两,故有“半斤八两”这个成语).设有 人分银子,根据题意所列方程正确的是( )A、 B、 C、 D、5. 如图,O为直线AB上一点,OM平分∠AOC , ON平分∠BOC , 则图中互余的角有( ) A、4对 B、3对 C、2对 D、1对6. , 都是钝角,有四名同学分别计算 ,却得到了四个不同的结果,分别为 , , , ,老师判作业时发现其中确有正确的结果,那么计算正确的结果是( )A、 B、 C、 D、7.
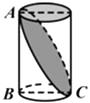
A、4对 B、3对 C、2对 D、1对6. , 都是钝角,有四名同学分别计算 ,却得到了四个不同的结果,分别为 , , , ,老师判作业时发现其中确有正确的结果,那么计算正确的结果是( )A、 B、 C、 D、7.如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
 A、
A、 B、
B、 C、
C、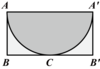 D、
D、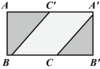 8. 若4个有理数 , , , 满足 , ,则下列大小关系一定成立的是( )A、 B、 C、 D、
8. 若4个有理数 , , , 满足 , ,则下列大小关系一定成立的是( )A、 B、 C、 D、二、填空题
-
9. 计算: .10. 写出一个单项式,使得它与多项式 的和为单项式:.11. 若 是关于 的方程 的解,则 的值为.12. 如图,在 中,∠C=90°,最长的边是.
 13. 如图,剪去四边形的“一角”,得到一个五边形,这个五边形的周长一定这个四边形的周长(填“大于”,“小于”或“等于”),依据是.
13. 如图,剪去四边形的“一角”,得到一个五边形,这个五边形的周长一定这个四边形的周长(填“大于”,“小于”或“等于”),依据是. 14. 如图, 是线段 上一点, , 分别是线段 , 的中点,若 , ,则 .
14. 如图, 是线段 上一点, , 分别是线段 , 的中点,若 , ,则 . 15. 螺旋测微器又称千分尺,用它测长度可以准确到 .它的读数方法是先读固定刻度,再读半刻度,若半刻度线已露出,记作 ,若半刻度线未露出,记作 ,再读可动刻度 ,记作 ,最终读数结果为固定刻度+半刻度+可动刻度+估读.例如图1的读数为 ,其中最后一位“6”为估读.则图2的读数为 .
15. 螺旋测微器又称千分尺,用它测长度可以准确到 .它的读数方法是先读固定刻度,再读半刻度,若半刻度线已露出,记作 ,若半刻度线未露出,记作 ,再读可动刻度 ,记作 ,最终读数结果为固定刻度+半刻度+可动刻度+估读.例如图1的读数为 ,其中最后一位“6”为估读.则图2的读数为 . 16. 鞋号是指鞋子的大小,中国于60年代后期,在全国测量脚长的基础上制定了“中国鞋号”,1998年政府发布了基于 系统,用毫米做单位的中华人民共和国国家标准 ,被称为“新鞋号”,之前以厘米为单位的鞋号从此被称为“旧鞋号”.新旧鞋号部分对应表如下:
16. 鞋号是指鞋子的大小,中国于60年代后期,在全国测量脚长的基础上制定了“中国鞋号”,1998年政府发布了基于 系统,用毫米做单位的中华人民共和国国家标准 ,被称为“新鞋号”,之前以厘米为单位的鞋号从此被称为“旧鞋号”.新旧鞋号部分对应表如下:新鞋号
220
225
230
235
…
270
旧鞋号
34
35
36
37
…
(1)、a的值为;(2)、若新鞋号为m,旧鞋号为n,则把旧鞋号转换为新鞋号的公式为三、解答题
-
17. 计算: .18. 计算: .19. 计算: .20. 0.5x-0.7=6.5-1.3x21. 解方程: .22. 若 , ,当 , 时,计算 的值.23. 如图, , 表示笔直的海岸边的两个观测点,从 地发现它的北偏东 方向有一艘船,同时,从 地发现这艘船在它的北偏东 方向.
 (1)、在图中画出这艘船的位置,并用点 表示;(2)、若此图的比例尺为1:100000,请你通过画图、测量,计算出这艘船到海岸线 的实际距离(精确到1千米).24. 判断一个正整数能被3整除的方法是:把这个正整数各个数位上的数字相加,如果所得的和能够被3整除,则这个正整数就能被3整除.请证明对于任意两位正整数,这个判断方法都是正确的.25. 小希准备在6年后考上大学时,用15000元给父母买一份礼物表示感谢,决定现在把零花钱存入银行下面有两种储蓄方案:
(1)、在图中画出这艘船的位置,并用点 表示;(2)、若此图的比例尺为1:100000,请你通过画图、测量,计算出这艘船到海岸线 的实际距离(精确到1千米).24. 判断一个正整数能被3整除的方法是:把这个正整数各个数位上的数字相加,如果所得的和能够被3整除,则这个正整数就能被3整除.请证明对于任意两位正整数,这个判断方法都是正确的.25. 小希准备在6年后考上大学时,用15000元给父母买一份礼物表示感谢,决定现在把零花钱存入银行下面有两种储蓄方案:①直接存一个6年期.(6年期年利率为 )
②先存一个3年期,3年后本金与利息的和再自动转存一个3年期.(3年期年利率为 )
你认为按哪种储蓄方案开始存入的本金比较少?请通过计算说明理由.
26. 阅读材料,并回答问题钟表中蕴含着有趣的数学运算,不用负数也可以作减法,例如现在是10点钟,4小时以后是几点钟?虽然 ,但在表盘上看到的是2点钟.如果用符号“⊕”表示钟表上的加法,则 .若问2点钟之前4小时是几点钟,就得到钟表上的减法概念,用符号“㊀”表示钟表上的减法.(注:我们用0点钟代替12点钟)由上述材料可知:
(1)、 , ;(2)、在有理数运算中,相加得零的两个数互为相反数,如果在钟表运算中沿用这个概念,则5的相反数是 , 举例说明有理数减法法则:减去一个数等于加上这个数的相反数,在钟表运算中是否仍然成立;(3)、规定在钟表运算中也有 ,对于钟表上的任意数字 , , ,若 ,判断 是否一定成立,若一定成立,说明理由;若不一定成立,写出一组反例,并结合反例加以说明.