北京市昌平区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-13 类型：期末考试

进入出卷网下载

一、单选题

1. 2019年10月1日上午盛大的国庆阅兵在天安门广场举行，总规模约为15000人.阅兵编59个方(梯)队和联合军乐团，各型飞机160余架、装备580台(套)，是近几次阅兵中规模最大的一次.将15000用科学记数法可表示为（）

A、 $1.5 \times 10^{4}$ B、 $0.15 \times 10^{5}$ C、 $1.5 \times 10^{5}$ D、 $15 \times 10^{3}$

查看试题解析
2. 一个几何体的表面展开图如图所示，这个几何体是（）

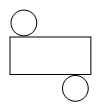A、正方体 B、三棱锥 C、四棱锥 D、圆柱

查看试题解析
3. 下列等式变形正确的是（）

A、如果a＝b，那么a＋3＝b－3 B、如果3a－7＝5a，那么3a＋5a＝7 C、如果3x＝－3，那么6x＝－6 D、如果2x＝3，那么x＝ $\frac{2}{3}$

查看试题解析
4. 有理数a，b在数轴上对应点的位置如图所示，下列说法中正确的是（）

A、a＞b B、﹣a＞b C、 $| a | > | b |$ D、a＋b＞0

查看试题解析
5. 下列运算正确的是（）

A、m²＋m³=m⁵ B、3m²－m²=2m C、3m²n－m²n＝2m²n D、m＋n=mn

查看试题解析
6. 若|m﹣3|+（n+2）²=0，则m+2n的值为（）

A、﹣1 B、1 C、4 D、7

查看试题解析
7. 在2019年世界杯上，中国女排最终以11战全胜积32分的成绩成功卫冕.比赛的积分规则为：比赛中以3-0或者3-1取胜的球队积3分、负队积0分，在比赛中以3-2取胜的球队积2分、负队积1分.某队以3-1胜了a场，以3-2胜了b场，以2-3负了c场，则该队的积分可表示为（）

A、3a＋2b＋c B、3a＋2b C、3a＋3b＋c D、3a＋3b

查看试题解析
8. 下图是昌平区2019年1月份每天的最低和最高气温，观察此图，下列说法正确的是（）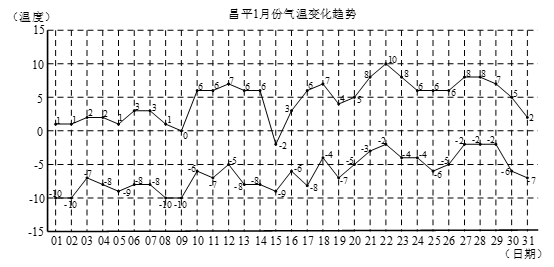

A、在1月份中，最高气温为10℃，最低气温为－2℃ B、在10号至16号的气温中，每天温差最小为7℃ C、每天的最高气温均高于0℃，最低气温均低于0℃ D、每天的最高气温与最低气温都是具有相反意义的量

查看试题解析

二、填空题

9. $| - 5 |$ 的相反数是．

查看试题解析
10. 单项式－2x²y的系数是，次数是.

查看试题解析
11. 如图，已知∠AOC=50°30′，∠BOC=14°18′，则∠AOB＝°′

查看试题解析
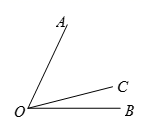12. 如果x=2是关于x的方程 $\frac{1}{2} x + m = 3$ 的解，那么m的值是.

查看试题解析
13. 一件商品的标价是100元，进价是50元，打八折出售后这件商品的利润是元.

查看试题解析
14. 如图，在四边形ABCD内找一点O，使它到四边形四个顶点的距离之和OA+OB+OC+OD最小，正确的作法是连接AC、BD交于点O，则点O就是要找的点，请你用所学过的数学知识解释这一道理.

查看试题解析
15. 代数式kx+b中，当x取值分别为－1,0,1,2时，对应代数式的值如下表：

x

－1

0

1

2

kx+b

－1

1

3

5

则k+b=.

查看试题解析
16. 在∠AOB中，C，D分别为边OA，OB上的点（不与顶点O重合）.对于任意锐角∠AOB，下面三个结论中，①作边OB的平行线与边OA相交，这样的平行线能作出无数条；②连接CD，存在∠ODC是直角；③点C到边OB的距离不超过线段CD的长.所有正确结论的序号是.

查看试题解析

三、解答题

17. 计算： $- 7 + (- 3) - 10 - (- 16)$

查看试题解析
18. 计算： $- 2.5 \div \frac{5}{8} \times (- \frac{1}{4})$ .

查看试题解析
19. 计算： $- 1^{4} + (- 2) \div (- \frac{1}{3}) - | - 9 |$ .

查看试题解析
20. 计算：(2－a²＋4a)－(5a²－a－1)

查看试题解析
21. 解方程： $5 x + 3 = 2 (x - 3)$ ．

查看试题解析
22. 解方程： $\frac{x + 2}{2} - \frac{x - 1}{3} = 1$

查看试题解析
23. 如图： A，B，C是平面上三个点，按下列要求画出图形.

(1)、作直线BC，射线AB，线段AC．

(2)、取AC中点D，连接BD，量出∠ACB的度数(精确到个位）.

(3)、通过度量猜想BD和AC的数量关系.

查看试题解析

24. 举世瞩目的2019年中国北京世界园艺博览会在长城脚下的北京延庆开园，它给人们提供了看山、看水、看风景的机会.一天小龙和朋友几家去延庆世园会游玩，他们购买普通票比购买优惠票的数量少5张，买票共花费了1400元，符合他们购票的条件如下表，请问他们买了多少张优惠票？

平

日

普通票

•适用所有人

•除指定日外任一平日参观

120

优惠票

•适用残疾人士、60周岁以上老年人、学生、中国现役军

人（具体人群规则同指定日优惠票）

•购票及入园时需出示相关有效证件

•除指定日外任一平日参观

查看试题解析

25. 如图：O是直线AB上一点，∠AOC＝50°，OD是∠BOC的角平分线，OE⊥OC于点O.求∠DOE的度数.（请补全下面的解题过程）

解：∵O是直线AB上一点，∠AOC＝50°，

∴∠BOC＝180°－∠AOC＝    ▲    °.

∵ OD是∠BOC的角平分线，

∴∠COD＝    ▲    ∠BOC.(    ▲    )

∴∠COD＝65°.

∵OE⊥OC于点O，（已知）.

∴∠COE＝    ▲    °.(    ▲    )

∴∠DOE＝∠COE－∠COD＝    ▲    °

查看试题解析
26. 已知线段AB，点C在直线AB上，D为线段BC的中点.

(1)、若AB＝8，AC＝2，求线段CD的长.

(2)、若点E是线段AC的中点，直接写出线段DE和AB的数量关系是.

查看试题解析
27. 观察下列两个等式： $1 - \frac{2}{3} = 2 \times 1 \times \frac{2}{3} - 1$ ， $2 - \frac{3}{5} = 2 \times 2 \times \frac{3}{5} - 1$ 给出定义如下：我们称使等式a﹣b＝2ab﹣1成立的一对有理数a，b为“同心有理数对”，记为（a，b），如：数对（1， $\frac{2}{3}$ ），（2， $\frac{3}{5}$ ），都是“同心有理数对”.

(1)、数对（﹣2，1），（3， $\frac{4}{7}$ ）是 “同心有理数对”的是.

(2)、若（a，3）是“同心有理数对”，求a的值；

(3)、若（m，n）是“同心有理数对”，则（﹣n，﹣m）“同心有理数对”（填“是”或“不是”），说明理由.

查看试题解析
28. 如图所示，点A，B，C是数轴上的三个点，其中AB＝12，且A，B两点表示的数互为相反数.

(1)、请在数轴上标出原点O，并写出点A表示的数；

(2)、如果点Q以每秒2个单位的速度从点B出发向左运动，那么经过秒时，点C恰好是BQ的中点；

(3)、如果点P以每秒1个单位的速度从点A出发向右运动，那么经过多少秒时PC＝2PB．

查看试题解析

x		－1	0	1	2
kx+b		－1	1	3	5