江苏省扬州市江都区八校2020-2021学年八年级上学期数学10月联考试卷
试卷更新日期：2020-11-12 类型：月考试卷
一、单选题
-
1. 下面四个手机应用图标中是轴对称图形的是（ ）
A、
B、
C、
D、
2. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，请你根据所学的图形的全等这一章的知识，说明画出∠A′O′B′=∠AOB的依据是（ ）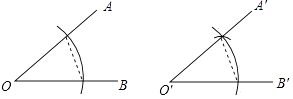
A、SAS B、ASA C、AAS D、SSS3. 到三角形三个顶点距离相等的点是（ ）A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点4. 如图，已知AD平分∠BAC，AB=AC，则此图中全等三角形有（ ）
A、2对 B、3对 C、4对 D、5对5. 如图，DE是AC边的垂直平分线，AB＝5cm，BC＝4cm.那△BEC的周长是（ ）
A、9cm B、8cm C、7cm D、6cm6. 三个全等三角形按如图的形式摆放，则∠1+∠2+∠3的度数是（ ）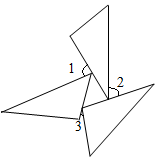
A、 B、 C、 D、7. 已知：如图在 ， 中， ， ， ，点C，D，E三点在同一条直线上，连接 ， .以下四个结论：① ；② ；③ ；④ ，其中结论正确的个数是（ ）.
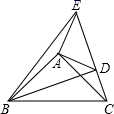A、1 B、2 C、3 D、4二、填空题
-
8. 在几何图形：等边三角形、正方形、正六边形和圆中，对称轴条数最多的是.9. 如图，在△ABC中，BC的垂直平分线分别交AB、BC于D、E，若△ACD的周长为10cm，AC=3cm，则AB= cm．
10. 如图，△ABC中，∠A=100°，∠B=20°，边BC的垂直平分线分别交AB、BC于点E、D，则∠ACE的度数等于.
11. 如图是4×4正方形网络，其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形，这样的白色小方格有个.
12. 如图，△ABE、△BDC 和△ABC 分别是关于 AB，BC 边所在直线对称的轴对称图形，若∠1：∠2：∠3=9：2：1，则∠4 的度数为.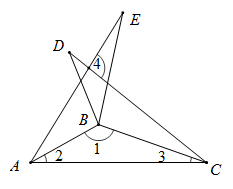
13. 如图，Rt△ABC中，∠BAC＝90°，AB＝AC ， 分别过点B、C作过点A的直线的垂线BD、CE ， 垂足分别为D、E ， 若BD＝3，CE＝2，则DE＝ ．
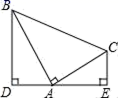14. 如图，在△ABC中，∠ACB=∠ABC=40o ， BD是∠ABC的角平分线，延长BD至点E，使得DE=DA，则∠ECA=.
15. 如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中，其两边分别与OA，OB相交于M、N两点，则以下结论：（1）PM＝PN恒成立，（2）OM＋ON的值不变，（3）四边形PMON的面积不变，（4）MN的长不变，其中正确的为（请填写结论前面的序号）.
三、解答题
-
16. 如图，在△ABC中， ∠BAC是钝角，按要求完成下列画图.
（不写作法，保留作图痕迹）
①用尺规作∠BAC的角平分线AE.
②用三角板作BC边上的高AD.
③用尺规作AB边上的垂直平分线.
17. 如图所示，在正方形网格上有一个△ABC.
（ 1 ）作△ABC关于直线MN的对称图形；（不写作法）
（ 2 ）在MN上找到一点P，使得PA+PC最小；
（ 3 ）若网格上的最小正方形边长为1，求△ABC的面积.
18. 已知：如图，AB=AE，∠1=∠2，∠B=∠E．求证：BC=ED．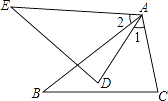
19. 如图，AD是△ABC的角平分线，∠B=90°，DF⊥AC，垂足为F，在AB上截取BE=CF.求证：△BDE≌△FDC
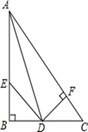20. 已知：如图所示，A、B、C、D在同一直线上，AD＝BC，AE＝BF，CE＝DF，试说明：
(1)、DF∥CE；(2)、DE＝CF.21. 如图：△ABC是等边三角形，点D、E分别是边BC、CA上的点，且BD=CE，AD、BE相交于点O.(友情提醒：等边三角形的三条边都相等，即AB＝AC＝BC；三个内角都是60°，即∠ABC＝∠BCA＝∠BAC＝60°)
(1)、求证：△ACD≌△BAE；(2)、求∠AOB的度数.22. 已知：如图∠BAC的角平分线与BC的垂直平分线交与点D，DE⊥AB，DF⊥AC，垂足分别为E，F．求证：BE=CF．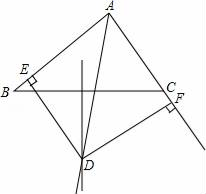
23. 如图，AB=AC，点D、E分别在AC、AB上，AG⊥BD，AF⊥CE，垂足分别为G、F，且AG=AF.
求证：
(1)、∠EAF=∠DAG；(2)、AD=AE.24. 在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E，
(1)、当直线MN绕点C旋转到图（1）的位置时，请你探究线段DE、AD、BE之间的数量关系并加以证明；(2)、当直线MN绕点C旋转到图（2）的位置时，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明.(3)、当直线MN绕点C旋转到图（3）的位置时，试问DE、AD、BE具有怎样的等量关系？请直接写出这个等量关系.25. 问题背景：如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝60°.探究图中线段BE，EF，FD之间的数量关系.
小王同学探究此问题的方法是，延长FD到点G.使DG＝BE.连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是什么；
探索延伸：
如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E，F分别是BC，CD上的点，且∠EAF＝ ∠BAD，上述结论是否仍然成立，并说明理由；
实际应用：
如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离.