江苏省南京市鼓楼区2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2020-11-12 类型:期中考试
一、单选题
-
1. 一元二次方程x2﹣4x﹣3=0的二次项系数、一次项系数和常数项分别是( )A、1,4,3 B、0,﹣4,﹣3 C、1,﹣4,3 D、1,﹣4,﹣32. 已知关于x的一元二次方程x2+bx﹣1=0,则下列关于该方程根的判断,正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关3. 有下列四个命题:
①经过三个点一定可以作圆②等弧所对的圆周角相等;③三角形的外心到三角形各顶点的距离都相等; ④在同圆中,平分弦的直径一定垂直于这条弦.其中正确的有( )
A、0 B、1 C、2 D、34. 如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )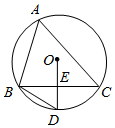 A、55° B、65° C、60° D、75°5. 如图,在 中, , , ,点P从点A开始沿AC边向点C以 的速度匀速移动,同时另一点Q由C点开始以 的速度沿着射线CB匀速移动,当 的面积等于 运动时间为
A、55° B、65° C、60° D、75°5. 如图,在 中, , , ,点P从点A开始沿AC边向点C以 的速度匀速移动,同时另一点Q由C点开始以 的速度沿着射线CB匀速移动,当 的面积等于 运动时间为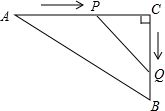 A、5秒 B、20秒 C、5秒或20秒 D、不确定6. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0).与y轴分别交于点B(0,4)与点C(0,16).则圆心M到坐标原点O的距离是( )
A、5秒 B、20秒 C、5秒或20秒 D、不确定6. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0).与y轴分别交于点B(0,4)与点C(0,16).则圆心M到坐标原点O的距离是( ) A、10; B、8 ; C、4 ; D、2 ;
A、10; B、8 ; C、4 ; D、2 ;二、填空题
-
7. 一元二次方程 有两个相等的实数根,则 .8. 用半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为.9. 设m , n是一元二次方程x2+2x-7=0的两个根,则m2+3m+n=.10. 一个两位数,个位数字比十位数字大3,个位数的平方恰好等于这个两位数,这个两位数是.11. 如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=
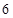 ,且AE:BE =1:3,则AB=.
,且AE:BE =1:3,则AB=.
 12. 如图,直线 a⊥b ,垂足为H,点P在直线b上, ,O为直线b上一动点,若以 为半径的 与直线a相切,则 的长为.
12. 如图,直线 a⊥b ,垂足为H,点P在直线b上, ,O为直线b上一动点,若以 为半径的 与直线a相切,则 的长为.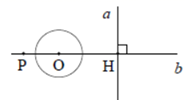 13. 如图,在 的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点,作 的外接圆,则 的长等于.
13. 如图,在 的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点,作 的外接圆,则 的长等于.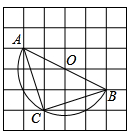 14. 一个三角形的两边长分别为2和5,第三边长是方程 的根,则该三角形的周长为.15. 疫情期间居民为了减少外出时间,大家更愿意使用APP在线上买菜,某买菜APP今年一月份新注册用户为200万,三月份新注册用户为338万,则二、三两个月新注册用户每月平均增长率是.16. 如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2 , 则r1:r2= .
14. 一个三角形的两边长分别为2和5,第三边长是方程 的根,则该三角形的周长为.15. 疫情期间居民为了减少外出时间,大家更愿意使用APP在线上买菜,某买菜APP今年一月份新注册用户为200万,三月份新注册用户为338万,则二、三两个月新注册用户每月平均增长率是.16. 如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2 , 则r1:r2= .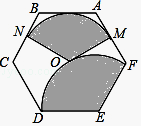
三、解答题
-
17. 解答下列各题:(1)、用配方法解方程: .(2)、已知一元二次方程 的一个根是 .求 的值和方程的另一个根.18. 已知:平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+ ﹣ =0的两个实数根.(1)、m为何值时,四边形ABCD是菱形?求出这时菱形的边长;(2)、若AB的长为2,那么▱ABCD的周长是多少?19. 如图1,有一张长 宽 的长方形硬纸片,裁去角上 个小正方形和 个小长方形(图中阴影部分)之后,恰好折成如图2的有盖纸盒.
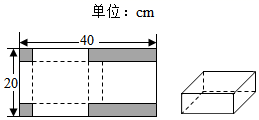 (1)、若纸盒的高是 cm,求纸盒底面长方形的长和宽;(2)、若纸盒的底面积是 ,求纸盒的高.20. 如图,⊙ 中,弦 与 相交于点E, ,连接 .
(1)、若纸盒的高是 cm,求纸盒底面长方形的长和宽;(2)、若纸盒的底面积是 ,求纸盒的高.20. 如图,⊙ 中,弦 与 相交于点E, ,连接 .
求证:
(1)、 ;(2)、 .21. 如图,在方格纸中,A,B,C三点都在小方格的顶点上(每个小方格的边长为1).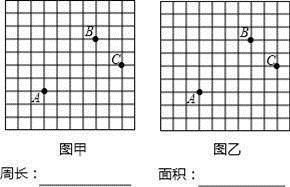
( 1 )在图甲中画一个以A,B,C为其中三个顶点的平行四边形,并求出它的周长.
( 2 )在图乙中画一个经过A,B,C三点的圆,并求出圆的面积.
22. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、若降价3元,则平均每天销售数量为件;(2)、当每件商品降价多少元时,该商店每天销售利润为1200元?23. 如图,四边形ABCD中,AB∥CD,点O在BD上,以O为圆心的圆恰好经过A、B、C三点,⊙O交BD于E,交AD于F,且 ,连接OA、OF.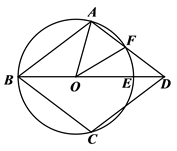 (1)、求证:四边形ABCD是菱形;(2)、若∠AOF=3∠FOE,求∠ABC的度数.24. 已知:如图, 为 的直径, 交 于点 , 交 于点 .
(1)、求证:四边形ABCD是菱形;(2)、若∠AOF=3∠FOE,求∠ABC的度数.24. 已知:如图, 为 的直径, 交 于点 , 交 于点 .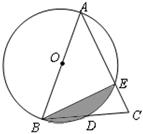 (1)、求 的大小;(2)、若 的半径为2,求图中阴影部分的面积.25. 阅读理解:
(1)、求 的大小;(2)、若 的半径为2,求图中阴影部分的面积.25. 阅读理解:材料一:若三个非零实数x , y , z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实教x , y , z构成“和谐三数组”.
材料二:若关于x的一元二次方程ax2+bx +c= 0(a≠0)的两根分别为 , ,则有 , .
问题解决:
(1)、请你写出三个能构成“和谐三数组”的实数;(2)、若 , 是关于x的方程ax2+bx +c= 0 (a , b , c均不为0)的两根, 是关于x的方程bx+c=0(b , c均不为0)的解.求证:x1 ,x2 , x3可以构成“和谐三数组”;(3)、若A(m , y1) ,B(m + 1,y2) ,C(m+3,y3)三个点均在反比例函数 的图象上,且三点的纵坐标恰好构成“和谐三数组”,求实数m的值.26. 如图,四边形 内接于圆, ,对角线 平分 .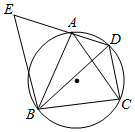 (1)、求证: 是等边三角形;(2)、过点 作 交 的延长线于点 ,若 ,求 的面积.27. 问题提出:
(1)、求证: 是等边三角形;(2)、过点 作 交 的延长线于点 ,若 ,求 的面积.27. 问题提出: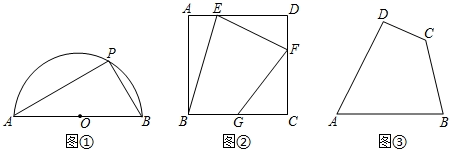 (1)、如图①,半圆O的直径AB=10,点P是半圆O上的一个动点,则△PAB的面积最大值是.(2)、问题探究:如图②,在边长为10的正方形ABCD中,点G是BC边的中点,E、F分别是AD和CD边上的点,请探究并求出四边形BEFG的周长的最小值.(3)、问题解决:如图③,四边形ABCD中,AB=AD=6,∠BAD=60°,∠BCD=120°,四边形ABCD的周长是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.
(1)、如图①,半圆O的直径AB=10,点P是半圆O上的一个动点,则△PAB的面积最大值是.(2)、问题探究:如图②,在边长为10的正方形ABCD中,点G是BC边的中点,E、F分别是AD和CD边上的点,请探究并求出四边形BEFG的周长的最小值.(3)、问题解决:如图③,四边形ABCD中,AB=AD=6,∠BAD=60°,∠BCD=120°,四边形ABCD的周长是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.