湖北省孝感市孝南区2020-2021学年七年级上学期数学10月月考试卷

试卷更新日期：2020-11-12 类型：月考试卷

进入出卷网下载

一、单选题

1. 如果将“收入 $100$ 元”记作“ $+100$ 元”，那么“支出 $50$ 元”应记作（） .

A、 $+50$ 元 B、 $- 50$ 元 C、 $+ 150$ 元 D、 $- 150$ 元

查看试题解析
2. 在下列选项中，既是分数，又是负数的是（）

A、9 B、 $\frac{1}{5}$ C、－0.125 D、－72

查看试题解析
3. 在有理数－1，0，－2，1中，最小的数是（　　）

A、－1 B、0 C、－2 D、1

查看试题解析
4. 如图，数轴上有A，B，C，D四个点，其中表示2的相反数的点是（）

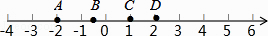A、点A B、点B C、点C D、点D

查看试题解析
5. 下列算式正确的是（）

A、(－14)－5=－9 B、0－(－3)=3 C、(－3)－(－3)=－6 D、 $| 5 - 3 | = - (5 - 3)$

查看试题解析
6. 将一把刻度尺按如图所示放在数轴上(数轴的单位长度是1cm)，刻度尺上的“0cm”和“8cm”分别对应数轴上的－3.6和x，则x的值为（）

A、4.2 B、4.3 C、4.4 D、4.5

查看试题解析
7. 下列说法中正确的是（　　）

A、一个有理数不是正数就是负数 B、|a|一定是正数 C、如果两个数的和是正数，那么这两个数中至少有一个正数 D、两个数的差一定小于被减数

查看试题解析
8. 有理数a，b在数轴上的位置如图所示，下列各式成立的是（）

A、b＞0 B、|a|＞－b C、a＋b＞0 D、ab＜0

查看试题解析
9. 若|a|＝5，b＝－3，则a－b的值为（）

A、2或8 B、－2或8 C、2或－8 D、－2或－8

查看试题解析
10. 在快速计算法中，法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”算法是完全一样的，而后面“六到九”的运算就改用手势了．如计算8×9时，左手伸出3根手指，右手伸出4根手指，两只手伸出手指数的和为7，未伸出手指数的积为2，则8×9=10×7+2=72．那么在计算6×7时，左、右手伸出的手指数应该分别为（　　）

A、1，2 B、1，3 C、4，2 D、4，3

查看试题解析

二、填空题

11. －3的相反数是，－2018的倒数是．

查看试题解析
12. 绝对值大于4而小于7的所有整数之和是.

查看试题解析
13. 点A，B表示数轴上互为相反数的两个数，且点A向左平移8个单位长度到达点B，则这两点所表示的数分别是和.

查看试题解析
14. 如果规定符号“※”的意义是：a※b= $\frac{a \cdot b}{a - b}$ ，那么3※(-3)的值为.

查看试题解析
15. 如图是一个简单的数值运算程序，当输入的 $x$ 的值为－1时，则输出的数值为.

查看试题解析
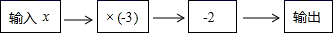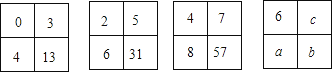
16.
填在下面各正方形中的四个数之间都有一定的规律，按此规律得出a+b+c= .

查看试题解析

三、解答题

17. 将下列各数在如图所示的数轴上表示出来，并用“＞”把这些数连接起来.
－1 $\frac{1}{2}$ ，0，2，－|－3|，－(－3.5).

查看试题解析
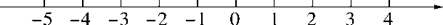18. 计算：

(1)、（－9）－（＋6）＋（－8）－（－10）

(2)、（－125 $\frac{5}{7}$ ）÷（－5）

(3)、（－24）× $(\frac{1}{2} - 1 \frac{1}{3} - \frac{3}{8})$ ；

(4)、－14－（ 1－ 0 × 4）÷ $\frac{1}{3}$ × [（－2）－6].

查看试题解析
19. 已知有理数a、b在数轴上的对应点如图所示，化简： |a＋b|＋|b|

查看试题解析
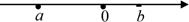20. 如果a，b互为相反数，c，d互为倒数，m的绝对值为2，求式子 $\frac{a + b}{a + b + c} + m^{2} - c d$ 的值.

查看试题解析
21. 某检修小组开车沿公路检修输电线路，约定前进为正，后退为负，某天自A地出发到收工时所走路径依次为(单位：千米)：
＋10、＋8、－7、＋12、－15、－9、＋16.

(1)、问收工时距A地多远；

(2)、若汽车每千米耗油0.08升，问从A地出发到收工时共耗油多少升.

查看试题解析
22. 根据某地实验测得的数据表明，高度每增加1 km，气温大约下降6℃，已知该地地面温度为21℃.

(1)、高空某处高度是8 km，求此处的温度是多少；

(2)、高空某处温度为一24 ℃，求此处的高度.

查看试题解析
23. 小明早晨跑步，他从自己家出发，向东跑了 $2 k m$ 到达小彬家，继续向东跑了 $1.5 k m$ 到达小红家，然后又向西跑了 $4.5 k m$ 到达学校，最后又向东，跑回到自己家.

(1)、以小明家为原点，以向东为正方向，用1个单位长度表示 $1 k m$ ，在图中的数轴上，分别用点A表示出小彬家，用点B表示出小红家，用点C表示出学校的位置；

(2)、求小彬家与学校之间的距离；

(3)、如果小明跑步的速度是每分钟0.25千米，那么小明这天早晨跑步一共用了多少分钟？

查看试题解析
24. 观察下列各式：
$- \frac{1}{1 \times 2} = - 1 + \frac{1}{2}$ ；

$- \frac{1}{2 \times 3} = - \frac{1}{2} + \frac{1}{3}$ −；

$- \frac{1}{3 \times 4} = - \frac{1}{3} + \frac{1}{4}$ ；

(1)、你发现的规律是 (用含n的式子表示)；

(2)、用规律计算：
$(- 1 \times \frac{1}{2}) + (- \frac{1}{2} \times \frac{1}{3}) + (- \frac{1}{3} \times \frac{1}{4}) + \dots + (- \frac{1}{2018} \times \frac{1}{2019}) + (- \frac{1}{2019} \times \frac{1}{2020})$ .

查看试题解析