陕西省武功县2021届九年级上学期数学第一次月考试卷
试卷更新日期:2020-11-12 类型:月考试卷
一、单选题
-
1. 在下列长度的各组线段中,能组成直角三角形的是( )A、5,6,7 B、5,12,13 C、1,4,9 D、5,11,122. 一元二次方程x2-8x-1=0配方后可变形为( )A、(x+4)2=17 B、(x+4)2=15 C、(x-4)2=17 D、(x-4)2=153. 如图,在 中, ,将 绕点A逆时针旋转 ,使点C落在点E处,点B落在点D处,则 两点间的距离为( )
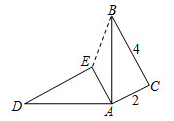 A、 B、 C、 D、4. 如图,菱形 中,E,F分别是 , 的中点,若 ,则菱形 的周长为( )
A、 B、 C、 D、4. 如图,菱形 中,E,F分别是 , 的中点,若 ,则菱形 的周长为( )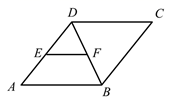 A、20 B、30 C、40 D、505. 如图,四边形 是正方形,O , D两点的坐标分别是 , ,点C在第一象限,则点C的坐标是( )
A、20 B、30 C、40 D、505. 如图,四边形 是正方形,O , D两点的坐标分别是 , ,点C在第一象限,则点C的坐标是( )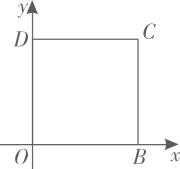 A、 B、 C、 D、6. 在矩形 中, 、 相交于点O,若 的面积为2,则矩形 的面积为( )
A、 B、 C、 D、6. 在矩形 中, 、 相交于点O,若 的面积为2,则矩形 的面积为( ) A、4 B、6 C、8 D、107. 不等式组 的解集在数轴上表示为( )A、
A、4 B、6 C、8 D、107. 不等式组 的解集在数轴上表示为( )A、 B、
B、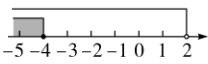 C、
C、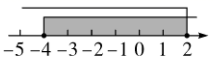 D、
D、 8. 如图,直线 与 ( 且a,b为常数)的交点坐标为(3,﹣1),则关于x的不等式 的解集为( )
8. 如图,直线 与 ( 且a,b为常数)的交点坐标为(3,﹣1),则关于x的不等式 的解集为( ) A、x≥﹣1 B、x≥3 C、x≤﹣1 D、x≤39. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
A、x≥﹣1 B、x≥3 C、x≤﹣1 D、x≤39. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )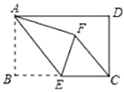 A、 B、 C、 D、10. 如图,在菱形 中, ,对角线 ,若过点A作 ,垂足为E,则 的长为( )
A、 B、 C、 D、10. 如图,在菱形 中, ,对角线 ,若过点A作 ,垂足为E,则 的长为( )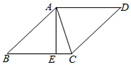 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若一元二次方程ax2﹣bx﹣2020=0有一根为x=﹣1,则a+b=.12. 关于x的一元二次方程x2+2x+k=0有两个不相等的实数根,则k的取值范围是 .13. 如图, ABCD的对角线AC,BD相交于点O,请添加一个条件: , 使 ABCD是菱形。
 14. 如图,在正方形 ABCD ,E是对角线 BD 上一点, AE 的延长线交 CD 于点F , 连接 CE .若∠BAE=56° ,则 ∠CEF= ° .
14. 如图,在正方形 ABCD ,E是对角线 BD 上一点, AE 的延长线交 CD 于点F , 连接 CE .若∠BAE=56° ,则 ∠CEF= ° .
三、解答题
-
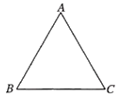
15. 用适当的方法解下列方程:16. 解方程 .17. 已知三角形ABC,用尺规求作一点P使PB=PC,且点P到AB,BC的距离相等(不写作法,保留痕迹)
 18. 先化简,再求值: ,其中19. 如图,在▱ABCD中, 平分 交 于点E, 平分 交 于点F.
18. 先化简,再求值: ,其中19. 如图,在▱ABCD中, 平分 交 于点E, 平分 交 于点F.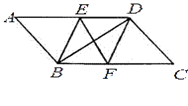
求证:
(1)、 ;(2)、若 ,则判断四边形 是什么特殊四边形,请证明你的结论.20. “a²≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式,例如: ,∵ ≥0,∴ ≥1,∴ ≥1,试利用“配方法”解决下列问题:(1)、填空:因为 (x)2+ , 所以当x=时,代数式 有最小值,这个最小值为;(2)、比较代数式 与 的大小.21. 如图,在矩形 中,过对角线 的中点O作 的垂线 ,分别交 于点 .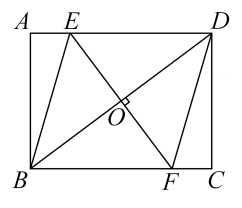 (1)、求证: ;(2)、若 ,连接 ,求四边形 的周长.22. 某单位计划从商店购买同一种品牌的钢笔和笔记本,已知购买一支钢笔比购买一个笔记本多用20元,若用1500元购买钢笔和用600元购买笔记本,则购买钢笔的数量是购买笔记本数量的一半.(1)、求购买一支钢笔、一个笔记本各需要多少元?(2)、经商谈,商店给予优惠,优惠方式是每购买一支钢笔赠送一个笔记本;如果此单位需要笔记本的数量是钢笔数量的3倍还少6个,且购买钢笔和笔记本的总费用不超过1020元,那么最多可购买多少支钢笔?23. 已知:如图,E是正方形ABCD的对角线BD上的点,连接AE、CE.
(1)、求证: ;(2)、若 ,连接 ,求四边形 的周长.22. 某单位计划从商店购买同一种品牌的钢笔和笔记本,已知购买一支钢笔比购买一个笔记本多用20元,若用1500元购买钢笔和用600元购买笔记本,则购买钢笔的数量是购买笔记本数量的一半.(1)、求购买一支钢笔、一个笔记本各需要多少元?(2)、经商谈,商店给予优惠,优惠方式是每购买一支钢笔赠送一个笔记本;如果此单位需要笔记本的数量是钢笔数量的3倍还少6个,且购买钢笔和笔记本的总费用不超过1020元,那么最多可购买多少支钢笔?23. 已知:如图,E是正方形ABCD的对角线BD上的点,连接AE、CE.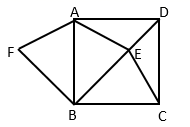 (1)、求证:AE=CE;(2)、若将△ABE沿AB翻折后得到△ABF,当点E在BD的何处时,四边形AFBE是正方形?请证明你的结论.24. 已知:关于x的方程 ,(1)、求证:无论k取任何实数值,方程总有实数根;(2)、若等腰三角形ABC的一边长a=1,两个边长b,c恰好是这个方程的两个根,求△ABC的周长.25. 受气候的影响,某超市蔬菜供应紧张,需每天从外地调运蔬菜1000斤.超市决定从甲、乙两大型蔬菜棚调运蔬菜,已知甲蔬菜棚每天最多可调出800斤,乙蔬菜棚每天最多可调运600斤,从两蔬菜棚调运蔬菜到超市的路程和运费如下表:
(1)、求证:AE=CE;(2)、若将△ABE沿AB翻折后得到△ABF,当点E在BD的何处时,四边形AFBE是正方形?请证明你的结论.24. 已知:关于x的方程 ,(1)、求证:无论k取任何实数值,方程总有实数根;(2)、若等腰三角形ABC的一边长a=1,两个边长b,c恰好是这个方程的两个根,求△ABC的周长.25. 受气候的影响,某超市蔬菜供应紧张,需每天从外地调运蔬菜1000斤.超市决定从甲、乙两大型蔬菜棚调运蔬菜,已知甲蔬菜棚每天最多可调出800斤,乙蔬菜棚每天最多可调运600斤,从两蔬菜棚调运蔬菜到超市的路程和运费如下表:到超市的路程(千米)
运费(元/斤·千米)
甲蔬菜棚
120
0.03
乙蔬菜棚
80
0.05
(1)、若某天调运蔬菜的总运费为3840元,则从甲、乙两蔬菜棚各调运了多少斤蔬菜?(2)、设从甲蔬菜棚调运蔬菜x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?