辽宁省铁岭市部分校2021届九年级上学期数学第一次月考试卷
试卷更新日期:2020-11-12 类型:月考试卷
一、单选题
-
1. 下列方程中,关于x的一元二次方程是( )A、 B、 C、 D、2. 用配方法解3x2﹣6x=6配方得( )A、(x﹣1)2=3 B、(x﹣2)2=3 C、(x﹣3)2=3 D、(x﹣4)2=33. 已知(x2+y2+1)(x2+y2+3)=8,则x2+y2的值为( )A、-5或1 B、1 C、5 D、5或-14. 若关于x的一元二次方程 有实数根,则a的取值范團是( )A、 B、 C、 D、5. 某机械厂七月份生产零件50万个,第三季度生产零件182万个.若该厂八、九月份平均每月生产零件的增长率均为x,则下面所列方程正确的是( )A、50(1+x)2=182 B、50+50(1+x)2=182 C、50+50(1+x)+50(1+2x)=182 D、50+50(1+x)+50(1+x)2=1826. 在四边形ABCD中,AC、BD交于点O,在下列各组条件中,不能判定四边形ABCD为矩形的是( )A、AB=CD,AD=BC,AC=BD B、AO=CO,BO=DO,∠A=90° C、∠A=∠C,∠B+∠C=180°,AC⊥BD D、∠A=∠B=90°,AC=BD7. 夹在两条平行线间的正方形ABCD、等边三角形DEF如图所示,顶点A,F分别在两条平行线上.若A,D,F在一条直线上,则∠1与∠2的数量关系是( )
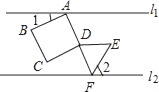 A、∠1+∠2=60° B、∠2﹣∠1=30° C、∠1=2∠2. D、∠1+2∠2=90°8. 如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为( )
A、∠1+∠2=60° B、∠2﹣∠1=30° C、∠1=2∠2. D、∠1+2∠2=90°8. 如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为( )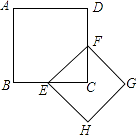 A、 B、2 C、 +1 D、2 +19. 如图,将矩形纸片 沿直线 折叠,使点C落在 边的中点 处,点B落在点 处,其中 ,则 的长为( )
A、 B、2 C、 +1 D、2 +19. 如图,将矩形纸片 沿直线 折叠,使点C落在 边的中点 处,点B落在点 处,其中 ,则 的长为( )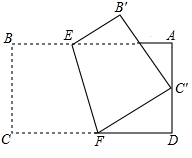 A、 B、4 C、4.5 D、510. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:
A、 B、4 C、4.5 D、510. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:
①OA=OD;
②AD⊥EF;
③当∠A=90°时,四边形AEDF是正方形;
④AE2+DF2=AF2+DE2.其中正确的是( )
A、②③ B、②④ C、①③④ D、②③④二、填空题
-
11. 方程 的根是.12. 等腰三角形两腰长分别为a,b,且a,b是关于x的一元二次方程x2﹣6x+n﹣1=0的两根,则n的值为.13. 关于x的一元二次方程 的解是 ,则方程 的解是.14. 如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为度.
 15. 在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是 .16. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,P为AB边上(不与A、B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是.
15. 在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是 .16. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,P为AB边上(不与A、B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是.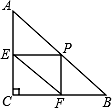 17. 已知,如图, ,作正方形 ,周长记作 ;再作第二个正方形 ,周长记作 ,继续作第三个正方形 ,周长记作 ;点 在射线 上,点 在射线 上,.依此类推,则第n个正方形的周长 =.
17. 已知,如图, ,作正方形 ,周长记作 ;再作第二个正方形 ,周长记作 ,继续作第三个正方形 ,周长记作 ;点 在射线 上,点 在射线 上,.依此类推,则第n个正方形的周长 =.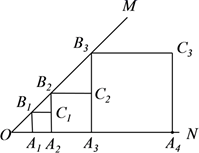 18. 关于x的方程(a﹣6)x2﹣8x+6=0有实数根,则整数a的最大值是 .
18. 关于x的方程(a﹣6)x2﹣8x+6=0有实数根,则整数a的最大值是 .
三、解答题
-
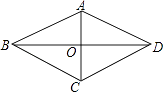
19. 用适当的方法解下列方程:(1)、(2)、20. 关于x的方程x2﹣ax+a+1=0有两个相等的实数根,求 的值.21. 如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.
 (1)、求证:四边形ABCD是菱形;(2)、若CD=3,BD=2 ,求四边形ABCD的面积.22. 已知方程 是关于 的一元二次方程.(1)、求证;对于任意实数 ,方程总有两个不相等的实数根;(2)、若方程的一个根是 ,求 的值及方程的另一个根.23. 已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)、求证:四边形ABCD是菱形;(2)、若CD=3,BD=2 ,求四边形ABCD的面积.22. 已知方程 是关于 的一元二次方程.(1)、求证;对于任意实数 ,方程总有两个不相等的实数根;(2)、若方程的一个根是 ,求 的值及方程的另一个根.23. 已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.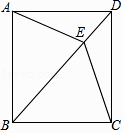 (1)、求证:四边形ABCD是菱形;(2)、如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.24. 某公司展销如图所示的长方形工艺品,该工艺品长 ,宽 ,中间镶有宽度相同的三条丝绸花边.
(1)、求证:四边形ABCD是菱形;(2)、如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.24. 某公司展销如图所示的长方形工艺品,该工艺品长 ,宽 ,中间镶有宽度相同的三条丝绸花边.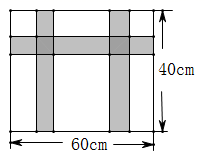 (1)、若丝绸花边的面积为 ,求丝绸花边的宽度;(2)、已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另外每天除工艺品的成本外所需支付的各种费用是2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,请问该公司每天把销售单价定为多少元所获利润为22500元.
(1)、若丝绸花边的面积为 ,求丝绸花边的宽度;(2)、已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另外每天除工艺品的成本外所需支付的各种费用是2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,请问该公司每天把销售单价定为多少元所获利润为22500元.