辽宁省鞍山市铁东区2021届九年级上学期数学第一次月考试卷

试卷更新日期：2020-11-12 类型：月考试卷

进入出卷网下载

一、单选题

1. 关于x的一元二次方程ax²+5x+3＝0有两个不相等的实数根，则实数a的取值范围是（）

A、a＜ $\frac{25}{12}$ 且a≠0 B、a＞ $\frac{25}{12}$ C、a≤ $\frac{25}{12}$ 且a≠0 D、a≥ $\frac{25}{12}$

查看试题解析
2. 将如图的七巧板的其中几块，拼成一个多边形，为中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 已知a，b是方程x²+（m+2）x+1=0的两根，则（a²+ma+1）（b²+mb+1）的值（）

A、4 B、1 C、-1 D、与m有关，无法确定

查看试题解析
4. 如图，在 $Δ A B C$ 中， $∠ B A C = 108 °$ ，将 $Δ A B C$ 绕点A按逆时针方向旋转得到 $Δ A B^{'} C^{'}$ .若点 $B^{'}$ 恰好落在 $B C$ 边上，且 $A B^{'} = C B^{'}$ ，则 $∠ C^{'}$ 的度数为（）

A、 $18 °$ B、 $20 °$ C、 $24 °$ D、 $28 °$

查看试题解析
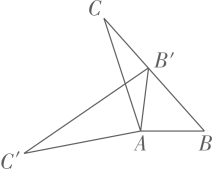5. 在同一直角坐标系中，a≠0，函数y＝ax与y＝ax²的图象可能正确的有（）

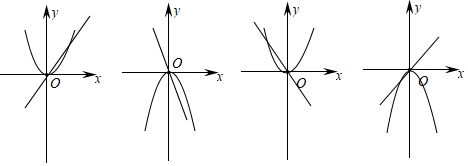A、0 B、1 C、2 D、3

查看试题解析
6. 如图，D在BC上，△ABC和△ADE均为等边三角形，AC与DE相交于点F，则图中相似三角形有（　　）

A、3对 B、4对 C、5对 D、6对

查看试题解析
7. 某班学生毕业时都将自己的照片向全班其他学生各送一张以作留念，全班共送出1056张照片.如果全班有x名同学，根据题意，列出的方程为（）

A、 $x (x + 1) = 1056$ B、 $x (x - 1) = 1056 \times 2$ C、 $x (x - 1) = 1056$ D、 $2 x (x + 1) = 1056$

查看试题解析
8. 如图，四边形ABCD为正方形，AB＝1，把△ABC绕点A逆时针旋转60°得到△AEF ，连接DF ，则DF的长为（）

A、 $\frac{\sqrt{6} - \sqrt{2}}{2}$ B、 $\frac{\sqrt{2} - 1}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析

二、填空题

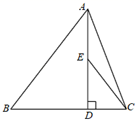
9. 若方程x²＋mx＋1＝0和x²＋x＋m＝0有公共根，则常数m的值是.

查看试题解析
10. 如图，在△ABC中，已知AB＝2，AD⊥BC，垂足为D，BD＝2CD.若E是AD的中点，则EC＝.

查看试题解析
11. 对于实数a，b，定义运算“*”，a*b＝ ${\begin{cases} a^{2} - a b (a > b) \\ a b - b^{2} (a \leq b) \end{cases}$ 例如4*2．因为4＞2，所以4*2＝4²－4×2＝8，若x₁、x₂是一元二次方程x²－9x＋20＝0的两个根，则x₁*x₂＝．

查看试题解析
12. 已知矩形ABCD，AB＝6，AD＝8，将矩形ABCD绕点A顺时针旋转θ（0°＜θ＜360°）得到矩形AEFG，当θ＝°时，GC＝GB.

查看试题解析
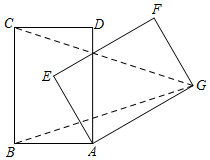13. 如图，⊙O的半径为2，C₁是函数y=2x²的图象，C₂是函数y=－2x²的图象，则图中阴影部分的面积为.

查看试题解析
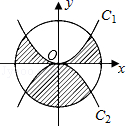14. 如图是一张矩形纸片，点E在AB边上，把 $△ B C E$ 沿直线CE对折，使点B落在对角线AC上的点F处，连接DF.若点E，F，D在同一条直线上，AE＝2，则DF＝， BE＝.

查看试题解析
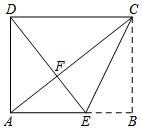15. 某种传染性牛疾在牛群中传播迅猛，平均一头牛每隔6小时能传染m头牛，现知一养牛场有a头牛染有此病，那么12小时后共有头牛染上此病（用含a、m的代数式表示）.

查看试题解析
16. 在直角三角形ABC中，∠ABC＝90°，∠BAC＝30°，BC＝2，P是AB边上一动点，则PC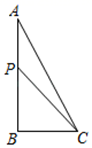+ $\frac{1}{2}$ AP的最小值为.

查看试题解析

三、解答题

17. 用适当的方法解下列方程

(1)、 $x^{2} - 4 x - 3 = 0$

(2)、 ${(x - 3)}^{2} + 2 x (x - 3) = 0$

(3)、 ${(x - 1)}^{2} = 4$

(4)、 $3 x^{2} + 5 (2 x + 1) = 0$

查看试题解析
18. 如图，△ABC的顶点坐标分别为A(0，1)，B(3，3)，C(1，3)，

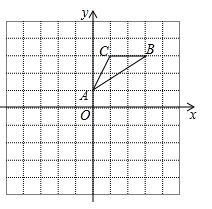(1)、①画出△ABC关于原点O的中心对称图形△A₁B₁C₁；
②画出△ABC绕原点O逆时针旋转90°得到的△A₂B₂C₂ ，写出点C₂的坐标；

(2)、若△ABC上任意一点P(m，n)绕原点O逆时针旋转90°的对应点为Q，则点Q的坐标为.(用含m，n的式子表示)

查看试题解析
19. 已知关于x的方程x²﹣（3k+3）x+2k²+4k+2＝0，

(1)、求证：无论k为何值，原方程都有实数根；

(2)、若该方程的两实数根x₁、x₂为一菱形的两条对角线之长，且x₁x₂+2x₁+2x₂＝36，求k值及该菱形的面积.

查看试题解析
20. 在Rt△ABC中，∠ABC=90°，∠BAC＝30°，将△ABC绕点A顺时针旋转一定的角度 $α$ 得到△AED ，点B、C的对应点分别是E、D.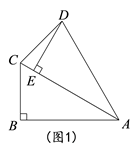

(1)、如图1，当点E恰好在AC上时，求∠CDE的度数；

(2)、如图2，若 $α$ =60°时，点F是边AC中点，求证：四边形BFDE是平行四边形.

查看试题解析
21. 去年某商店“十一黄金周”进行促销活动期间，前六天的总营业额为450万元，第七天的营业额是前六天总营业额的12%．

(1)、求该商店去年“十一黄金周”这七天的总营业额；

(2)、去年，该商店7月份的营业额为350万元，8、9月份营业额的月增长率相同，“十一黄金周”这七天的总营业额与9月份的营业额相等．求该商店去年8、9月份营业额的月增长率．

查看试题解析
22. 如图，在△ABC中，点D，E，F分别在AB，BC，AC边上，DE∥AC，EF∥AB.

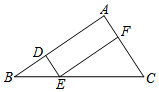(1)、求证：△BDE∽△EFC.

(2)、设 $\frac{A F}{F C} = \frac{1}{2}$ ，
①若BC＝12，求线段BE的长；

②若△EFC的面积是20，求△ABC的面积.

查看试题解析
23. “疫情”期间，李晨在家制作一种工艺品，并通过网络平台进行线上销售.经过一段时间后发现：当售价是40元/件时，每天可售出该商品60件，且售价每降低1元，就会多售出3件，设该商品的售价为x元/件（20≤x≤40）.

(1)、请用含售价x（元/件）的代数式表示每天能售出该工艺品的件数；

(2)、已知每件工艺品需要20元成本，每天销售该工艺品的纯利润为900元.
①求该商品的售价；

②为了支持“抗疫”行动，李晨决定每销售一件该工艺品便通过网络平台自动向某救助基金会捐款0.5元，求李晨每天通过销售该工艺品捐款的数额.

查看试题解析
24.

(1)、（基础巩固）
如图1，在△ABC中，D为AB上一点，∠ACD＝∠B.求证：AC²＝AD•AB.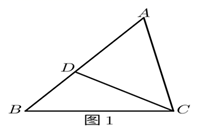

(2)、（尝试应用）
如图2，在▱ABCD中，E为BC上一点，F为CD延长线上一点，∠BFE＝∠A.若BF＝4，BE＝3，求AD的长.

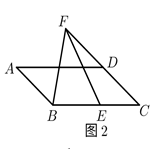(3)、（拓展提高）
如图3，在菱形ABCD中，E是AB上一点，F是△ABC内一点，EF∥AC，AC＝2EF，∠EDF＝ $\frac{1}{2}$ ∠BAD，AE＝2，DF＝5，求菱形ABCD的边长.

查看试题解析
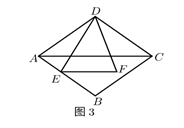25. 如图所示，抛物线y₁＝﹣x²与直线y₂＝﹣ $\frac{3}{2}$ x﹣ $\frac{9}{2}$ 交于A，B两点.

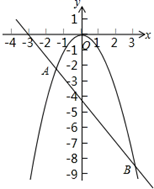(1)、求A，B两点的坐标.

(2)、根据图象回答：
①当x取何值时，y₁的值随x的增大而增大？

②当x取何值时，y₁＜y₂？

(3)、求△AOB的面积.

(4)、在x轴上是否存在一点P，使△AOP是等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由.

(5)、抛物线上找一点Q，使得△ABQ是直角三角形，请直接写出Q点横坐标

查看试题解析