广西河池市2019-2020学年高一上学期数学期末考试试卷
试卷更新日期:2020-11-12 类型:期末考试
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 圆 的半径为( )A、4 B、 C、11 D、3. 已知 , , 则( )A、 B、 C、 D、4. 函数 的图象恒过定点M,则M的坐标为( )A、(-1,3) B、(0,3) C、(3,-1) D、(3,0)5. 若函数 的零点所在的区间为 ,则k=( )A、3 B、4 C、1 D、26. 若函数 ,则 ( )A、9 B、6 C、4 D、37. 点 到直线 的距离的最小值为( )A、4 B、 C、 D、8. 已知l,m是两条不同的直线, , 是两个不同的平面,且 , ,现有下列命题:①若 ,则 ;②若 ,则 ;③若 ,则 ④若 ,则 .
其中正确的命题个数为( )
A、1 B、2 C、3 D、49. 某几何体的三视图如图所示,则该几何体的最长棱的长为( )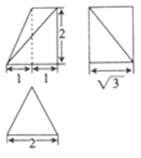 A、4 B、 C、 D、10. 把边长为 的正方形 沿对角线 折起,当直线 和平面 所成的角为 时,三棱锥 的体积为( )A、 B、 C、 D、11. 已知 是定义在 上的奇函数,且 在 上单调递减,则不等式 的解集为( )A、 B、 C、 D、12. 棱长为a的正四面体ABCD与正三棱锥 的底面重合,若由它们构成的多面体ABCDE的顶点均在一球的球面上,则正三棱锥 的表面积为( )A、 B、 C、 D、
A、4 B、 C、 D、10. 把边长为 的正方形 沿对角线 折起,当直线 和平面 所成的角为 时,三棱锥 的体积为( )A、 B、 C、 D、11. 已知 是定义在 上的奇函数,且 在 上单调递减,则不等式 的解集为( )A、 B、 C、 D、12. 棱长为a的正四面体ABCD与正三棱锥 的底面重合,若由它们构成的多面体ABCDE的顶点均在一球的球面上,则正三棱锥 的表面积为( )A、 B、 C、 D、二、填空题
-
13. 已知直线AB的斜率为1,则直线AB的倾斜角为.14. 若幂函数 在 上单调递增,则 .15. 已知集合 , , ,则实数a的取值的集合为.16. 设函数 ,则 .
三、解答题
-
17. 在四面体ABCD中, 与 都是边长为8的正三角形,点O是线段BC的中点.
 (1)、证明: .(2)、若 为锐角,且四面体ABCD的体积为 求侧面ACD的面积.18. 计算或化简:(1)、 ;(2)、 .19. 直线 : 与坐标轴的交点为 , ,以线段 为直径的圆 经过点 .(1)、求圆 的标准方程;(2)、若直线 : 与圆 交于 , 两点,求 .
(1)、证明: .(2)、若 为锐角,且四面体ABCD的体积为 求侧面ACD的面积.18. 计算或化简:(1)、 ;(2)、 .19. 直线 : 与坐标轴的交点为 , ,以线段 为直径的圆 经过点 .(1)、求圆 的标准方程;(2)、若直线 : 与圆 交于 , 两点,求 .
