河南省上蔡县重点中学2020年数学中考模拟试卷
试卷更新日期:2020-11-11 类型:中考模拟
一、选择题
-
1. 如图所示,点A,B,C在数轴上的位置如图所示,O为原点,C表示的数为m, , ,则A表示的数为( )
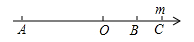 A、 B、 C、 D、2. 夸克是组成质子和中子(及其他许多粒子)的粒子,1夸克长度约为 ,一根头发丝的横截面约为0.06mm,则一根头发丝等于个夸克并排放在一起的宽度( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 如图1、图2、图3所示,下列说法错误的是( )
A、 B、 C、 D、2. 夸克是组成质子和中子(及其他许多粒子)的粒子,1夸克长度约为 ,一根头发丝的横截面约为0.06mm,则一根头发丝等于个夸克并排放在一起的宽度( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 如图1、图2、图3所示,下列说法错误的是( )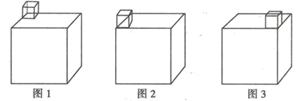 A、图1的主视图和图2的主视图相同 B、图2的左视图和图3的主视图相同 C、图1的左视图和图2的主视图相同 D、图3的左视图和图2的主视图相同5. 下列运动属于旋转的是( )A、火箭升空的运动 B、足球在草地上滚动 C、大风车运动的过程 D、传输带运输的东西6. 小丽要作 的平分线,她用了以下作法:①在平面内任取一点P;②以P为圆心,PO为半径作圆,交OA于D,交OB于E;③连接DE,过P作 交 于C;④连接OC.则小丽作图的依据不包括下列哪条( )
A、图1的主视图和图2的主视图相同 B、图2的左视图和图3的主视图相同 C、图1的左视图和图2的主视图相同 D、图3的左视图和图2的主视图相同5. 下列运动属于旋转的是( )A、火箭升空的运动 B、足球在草地上滚动 C、大风车运动的过程 D、传输带运输的东西6. 小丽要作 的平分线,她用了以下作法:①在平面内任取一点P;②以P为圆心,PO为半径作圆,交OA于D,交OB于E;③连接DE,过P作 交 于C;④连接OC.则小丽作图的依据不包括下列哪条( )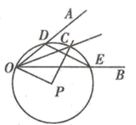 A、垂经定理 B、同弧或等弧所对的圆周角相等 C、在同圆或等圆中相等的圆周角所对的弧相等 D、角平分线定义7. 暑假期间,“精英”班将组织学生进行研学活动,小雨和小雪两个同学要从“红色抗战足迹”“故宫历史遗迹”“科技成果展览”三个活动中各选择一个参加,则两人恰好选择同一个研学活动的概率是( )A、 B、 C、 D、8. 已知关于x的分式方程 的解为正数,则k的取值范围是( )A、 B、 且 C、 D、 且9. 如图所示, 与 的图象交于 , 两点,则不等式 的解集为( )
A、垂经定理 B、同弧或等弧所对的圆周角相等 C、在同圆或等圆中相等的圆周角所对的弧相等 D、角平分线定义7. 暑假期间,“精英”班将组织学生进行研学活动,小雨和小雪两个同学要从“红色抗战足迹”“故宫历史遗迹”“科技成果展览”三个活动中各选择一个参加,则两人恰好选择同一个研学活动的概率是( )A、 B、 C、 D、8. 已知关于x的分式方程 的解为正数,则k的取值范围是( )A、 B、 且 C、 D、 且9. 如图所示, 与 的图象交于 , 两点,则不等式 的解集为( )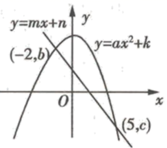 A、 B、 或 C、 D、 或10. 如图所示,MN是半圆O的直径,MP与半圆O相切于点M,R是半圆上一动点, 于E,连接MR.设 , ,则下列函数图象能反映y与x之间关系的是( )
A、 B、 或 C、 D、 或10. 如图所示,MN是半圆O的直径,MP与半圆O相切于点M,R是半圆上一动点, 于E,连接MR.设 , ,则下列函数图象能反映y与x之间关系的是( ) A、
A、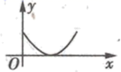 B、
B、 C、
C、 D、
D、
二、填空题
-
11. .12. 不等式组 的所有整数解的和为.13. 已知关于x的一元二次方程 有两个相等的实数根,则 的值为.14. 等腰 中, , , ,P是 内一点且 ,当PD最小时,此时 的面积为.
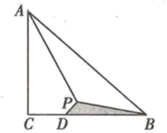 15. 如图所示,E、F、G分别是矩形ABCD的边AB、AD、BC上的点,GF与CE交于点O,且 , , ,则 的值为.
15. 如图所示,E、F、G分别是矩形ABCD的边AB、AD、BC上的点,GF与CE交于点O,且 , , ,则 的值为.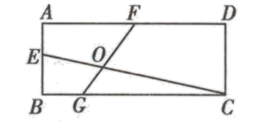
三、解答题
-
16. 先化简,再求值: ,其中x是方程 的一个根.17. 已知:如图所示,MN是 的直径,B是 上一点,NP平分 交 于P,过P作 于A.
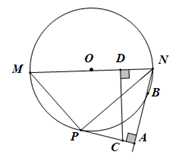 (1)、求证:PA与 相切;(2)、若 , ,求MP的长;(3)、若D是ON中点,过D作 交AP于C,若 , ,求 的半径.18. 2019年底,2020年初我国爆发了新冠肺炎疫情,为了增加学生对疫情和肺炎的预防知识的了解,某学校利用网络开展了相关知识的宣传教育活动,为了解这次的宣传效果,学校从全校3600名学生中随机抽取200名学生进行知识测试(满分100分,得分均为整数),并根据这200人的测试成绩,制订如下统计图表:
(1)、求证:PA与 相切;(2)、若 , ,求MP的长;(3)、若D是ON中点,过D作 交AP于C,若 , ,求 的半径.18. 2019年底,2020年初我国爆发了新冠肺炎疫情,为了增加学生对疫情和肺炎的预防知识的了解,某学校利用网络开展了相关知识的宣传教育活动,为了解这次的宣传效果,学校从全校3600名学生中随机抽取200名学生进行知识测试(满分100分,得分均为整数),并根据这200人的测试成绩,制订如下统计图表:
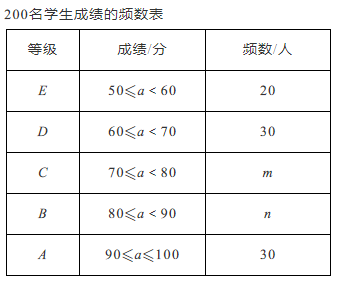
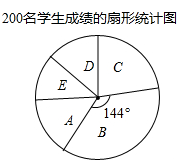 (1)、m=▲ , n=▲ , 成绩最好的等级A所占的百分比;(2)、张亮在这次测试中成绩为85分,你认为85分一定是这200名学生知识测试成绩的中位数吗?请简要说明理由;(3)、如果80分以上(包括80分)为优秀,请估计全校3600名学生中成绩优秀的人数.19. 如图所示,M、N、P在第二象限,横坐标分别是-4、-2、-1,双曲线 过M、N、P三点,且 .
(1)、m=▲ , n=▲ , 成绩最好的等级A所占的百分比;(2)、张亮在这次测试中成绩为85分,你认为85分一定是这200名学生知识测试成绩的中位数吗?请简要说明理由;(3)、如果80分以上(包括80分)为优秀,请估计全校3600名学生中成绩优秀的人数.19. 如图所示,M、N、P在第二象限,横坐标分别是-4、-2、-1,双曲线 过M、N、P三点,且 . (1)、求双曲线的解析式;(2)、过P点的直线l交X轴于A,交y轴于B,且 ,且交 于另一点Q,求Q点坐标;(3)、以PN为边(顺时针方向)作正方形 ,平移正方形使N落在x轴上,点P、E对应的点 、 正好落在反比例函数 上,求F对应点 的坐标.20. 图1是一台实物投影仪,图2是它的示意图,折线OMN表示固定支架,OM垂直水平桌面OP,点N为旋转点,EN可以旋转,当EN绕点N逆时针旋转时,投影探头EF始终垂直于水平桌面OP,经测量: , , , .(结果精确到0.1cm)
(1)、求双曲线的解析式;(2)、过P点的直线l交X轴于A,交y轴于B,且 ,且交 于另一点Q,求Q点坐标;(3)、以PN为边(顺时针方向)作正方形 ,平移正方形使N落在x轴上,点P、E对应的点 、 正好落在反比例函数 上,求F对应点 的坐标.20. 图1是一台实物投影仪,图2是它的示意图,折线OMN表示固定支架,OM垂直水平桌面OP,点N为旋转点,EN可以旋转,当EN绕点N逆时针旋转时,投影探头EF始终垂直于水平桌面OP,经测量: , , , .(结果精确到0.1cm)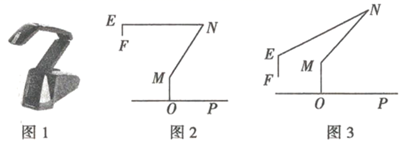 (1)、如图2所示, , .
(1)、如图2所示, , .①填空: ▲;
②求投影探头的端点 到桌面 的距离;
(2)、如图3所示,将(1)中的EN向下旋转,当投影探头的端点F到桌面OP的距离为 时,求 的大小.(参考数据 )21. 当今社会人们越来越离不开网络,电脑、手机被普遍使用,与此同时人们的视力也大大受到影响,2019年初某企业以25万元购得某项护目镜生产技术后,再投人100万元购买生产设备,进行该护目镜的生产加工,已知生产这种护目镜的成本价为每件20元,经过市场调研发现该产品的销售单价定在 元比较合理,并且该产品的年销售量 (万件)与销售单价 (元)之间的函数关系式为 .(年获利=年销售收入-生产成本-投资成本)(1)、求该公司第一年的年获利W(万元)与销售单价x(元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?(2)、2020年初我国爆发新冠肺炎,该公司决定向红十字会捐款20万元,另外每销售一件产品,就抽出1元钱作为捐款,若除去第一年的最大盈利(或最小亏损)以及第二年的捐款后,到2020年底,两年的总盈利不低于57.5万元,请你确定此时销售单价的范围.22. 如图 (1)、问题引入:如图1所示,正方形 和正方形 ,则 与 的数量关系是 , ;(2)、类比探究:如图2所示,O为AD、HG的中点,正方形EFGH和正方形ABVD中,判断BE和CF的数量关系,并求出 的值.(3)、解决问题:
(1)、问题引入:如图1所示,正方形 和正方形 ,则 与 的数量关系是 , ;(2)、类比探究:如图2所示,O为AD、HG的中点,正方形EFGH和正方形ABVD中,判断BE和CF的数量关系,并求出 的值.(3)、解决问题:①若把(1)中的正方形都改成矩形,且 ,则(1)中的结论还成立吗?若不能成立,请写出BE与GD的关系,并求出 的值;
②若把(2)中的正方形也都改成矩形,且 ,请直接写出BE和CF的关系以及 的值.
23. 如图所示,抛物线 的图象过 , , 三点,顶点为P.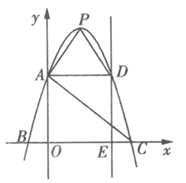 (1)、求抛物线的解析式;(2)、设点G在y轴上,且 ,求AG的长;(3)、若 轴且 在抛物线上,过 作 于 , 在直线 上运动,点 在 轴上运动,是否存在这样的点 、 使以 、 、 为顶点的三角形与 相似?若存在,请求出点 、 的坐标.
(1)、求抛物线的解析式;(2)、设点G在y轴上,且 ,求AG的长;(3)、若 轴且 在抛物线上,过 作 于 , 在直线 上运动,点 在 轴上运动,是否存在这样的点 、 使以 、 、 为顶点的三角形与 相似?若存在,请求出点 、 的坐标.