浙江省宁波市普通高中2020年保送生模拟测试数学试卷
试卷更新日期:2020-11-11 类型:中考模拟
一、选择题(每题5分,共25分.)
-
1. 已知非零实数a、b、c满足ab= (a+b) ,bc= (b+c) ,ca= (c+a) ,则 =( )A、1 B、3 C、4 D、62. Rt△ABC中,∠ABC=90°,∠BAC=60°,点D为AC上一点,且AD︰CD=1︰4,过点D作DE⊥BC,垂足为点E,连接AE,则tan∠AEB的值为( )A、 B、 C、 D、3.
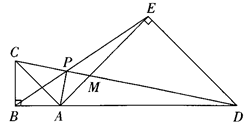
如图,点A在线段BD上,在 BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE、AE分别交于点P、M.对于下列结论:
①△BAE∽△CAD;②MP•MD=MA•MA;③2CB2=CP•CM.其中正确的是( )
A、①②③ B、① C、①② D、②③4. 如图,菱形ABCD中,对角线AC,BD相交于点O,AC=12cm,BD=16cm,动点N从点D出发,沿线段DB以2cm/s的速度向点B运动,同时动点M从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随之停止,设运动时间为t(s)(t>0),以点M为圆心,MB长为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.若⊙M与线段EN只有一个公共点,则t的取值范围为( )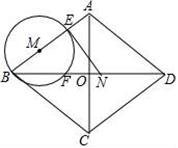 A、0<t≤ 或 <t<6 B、0<t≤ 或 <t<8 C、0<t≤ 或 <t<6 D、0<t≤ 或 <t<85. 设实数x>0,y>0,且x+y-2x2y2=4,则 的最小值为( )A、4 B、3 C、2 D、
A、0<t≤ 或 <t<6 B、0<t≤ 或 <t<8 C、0<t≤ 或 <t<6 D、0<t≤ 或 <t<85. 设实数x>0,y>0,且x+y-2x2y2=4,则 的最小值为( )A、4 B、3 C、2 D、二、填空题 (每题5分,共20分)
-
6. 若 ,则 (1- )÷(x-4+ ) 的值为 .7. 如图,4张卡片A、B、C、D的正面分别画有4个不同的图形(背面相同) ,将这4张卡片洗均匀后倒扣在桌面上,小王和小李轮流从中抽出1张卡片(放回) .若两人抽出的卡片不同,但两张卡片上的图形是轴对称图形又是中心对称图形的概率为 .
 8. 在平面直角坐标系xOy中,点A是x轴外一点,若平面内的点B满足:线段AB的长度与点A到x轴的距离相等,则称点B是点A的“等距点” .已知⊙P的半径为2,圆心为P(0,t) ,在函数y= x(x>0) 的图象上存在点M,⊙P上存在点N,满足点N是点M的“等距点” ,则t的取值范围为 .9. 设a、b、c、d是4个两两不同的实数,若a、b是方程x2-8cx-9d=0的解,c、d是方程x2-8ax-9b=0的解,则a+b+c+d的值为 .
8. 在平面直角坐标系xOy中,点A是x轴外一点,若平面内的点B满足:线段AB的长度与点A到x轴的距离相等,则称点B是点A的“等距点” .已知⊙P的半径为2,圆心为P(0,t) ,在函数y= x(x>0) 的图象上存在点M,⊙P上存在点N,满足点N是点M的“等距点” ,则t的取值范围为 .9. 设a、b、c、d是4个两两不同的实数,若a、b是方程x2-8cx-9d=0的解,c、d是方程x2-8ax-9b=0的解,则a+b+c+d的值为 .三、解答题(每題15分,共30分)