浙江省湖州市吴兴区2020年数学中考一模试卷
试卷更新日期:2020-11-11 类型:中考模拟
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 在 这四个数中,最小的数是( )A、 B、0 C、-3 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 小刚和小亮分别统计了自己最近50次跳绳成绩,下列统计量中能用来比较两人成绩稳定程度的是( )A、方差 B、中位数 C、平均数 D、众数4. 一个布袋里装有2个白球和3个黑球,它们除颜色外其余都相同,从袋子里任意摸出1个球,摸到黑球的概率是( )A、 B、 C、 D、15. 在Rt△ABC中,∠C=90°,AC=3,BC=4,tanB=( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、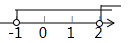 C、
C、 D、
D、 7. 如图,在平面直角坐标系中,正方形 ABCO 的顶点 A,C 分别在 y 轴、x 轴上,以 AB 为弦的⊙M 与 x 轴相切,若点 A 的坐标(0,8),则圆心M 的坐标为( )
7. 如图,在平面直角坐标系中,正方形 ABCO 的顶点 A,C 分别在 y 轴、x 轴上,以 AB 为弦的⊙M 与 x 轴相切,若点 A 的坐标(0,8),则圆心M 的坐标为( )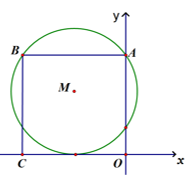 A、(-4,3) B、(-3,4) C、(-5,5) D、(-4,5)8. 抛物线经过点A(2,0),B(−1,0),且与y轴交于点C,若OC=2.则该抛物线解析式为( )A、 B、 或 C、 D、9. 如图,以矩形OABC的两边OA和OC所在直线为x轴、y轴建立平面直角坐标系。将矩形OABC绕点O逆时针旋转30°,得到矩形ODEF,若当点A的坐标为(- , 0)时,反比例函数的图象恰好经过B、F两点,则此时k的值为( ).
A、(-4,3) B、(-3,4) C、(-5,5) D、(-4,5)8. 抛物线经过点A(2,0),B(−1,0),且与y轴交于点C,若OC=2.则该抛物线解析式为( )A、 B、 或 C、 D、9. 如图,以矩形OABC的两边OA和OC所在直线为x轴、y轴建立平面直角坐标系。将矩形OABC绕点O逆时针旋转30°,得到矩形ODEF,若当点A的坐标为(- , 0)时,反比例函数的图象恰好经过B、F两点,则此时k的值为( ).
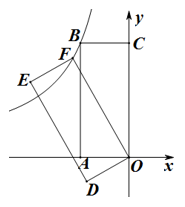
A、 B、-6 C、 D、-310. 如图,在矩形ABCD中,点E,F将对角线AC三等分,已知 AB=9,BC=12,点P在矩形ABCD的边上,则满足PE+PF=12的点P的个数是( )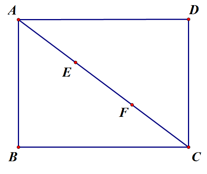 A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8二、填空题(本题有6小题,每小题4分,共24分)
-
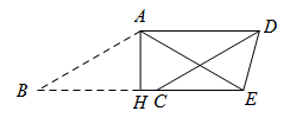
11. 8的立方根为.12. 因式分解: = .13. 一个扇形的半径是12cm,面积是 ,则此扇形的圆心角的度数是 .14. 如图所示,把菱形ABCD沿折痕AH翻折,使B点落在BC延长线上的点E处,连结DE.若∠B=30°,则∠ADE= .
 15. 正方形ABCD,点E在BC上,点F在CD上,且BE=CF.连结AE,BF,两线相交于点G,已知正方形边长为 ,△ABG的周长为 ,则图中阴影部分与空白部分的面积比为.
15. 正方形ABCD,点E在BC上,点F在CD上,且BE=CF.连结AE,BF,两线相交于点G,已知正方形边长为 ,△ABG的周长为 ,则图中阴影部分与空白部分的面积比为. 16. 在滑草过程中,小明发现滑道两边形如两条双曲线。如图,点A1 , A2 , A3…在反比例函数 的图象上,点B1 , B2 , B3…在反比例函数 的图象上, A1B1//A2B2…//y轴,已知点A1 , A2…的横坐标分别为1 , 2 …,令四边形A1B1B2A2、A2B2B3A3、 …的面积分别为S1、S2、…
16. 在滑草过程中,小明发现滑道两边形如两条双曲线。如图,点A1 , A2 , A3…在反比例函数 的图象上,点B1 , B2 , B3…在反比例函数 的图象上, A1B1//A2B2…//y轴,已知点A1 , A2…的横坐标分别为1 , 2 …,令四边形A1B1B2A2、A2B2B3A3、 …的面积分别为S1、S2、…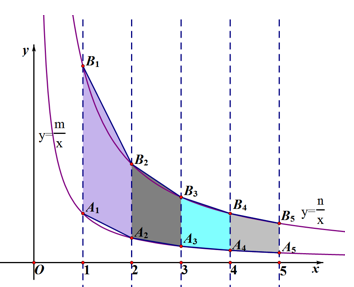 (1)、用含m、n的代数式表示S1= .(2)、若S20=41,则n-m= .
(1)、用含m、n的代数式表示S1= .(2)、若S20=41,则n-m= .三、解答题(本题有8小题,共66分)
-
17. 计算:
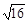 +(
+( 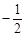 )
) 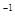 +
+ 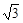 cos30°. 18. 解方程:19. 如图,一次函数 的图象与x轴,y轴分别交于A(-12,0),B(0,6)两点。
cos30°. 18. 解方程:19. 如图,一次函数 的图象与x轴,y轴分别交于A(-12,0),B(0,6)两点。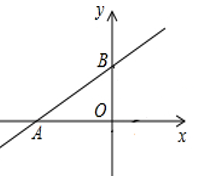 (1)、求一次函数的解析式;(2)、若C为x轴上任意一点,使得△ABC的面积为6求点C的坐标;20. 某报社为调查湖州市民对大范围雾霾天气的成因、影响以及应对措施的了解程度,做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题.
(1)、求一次函数的解析式;(2)、若C为x轴上任意一点,使得△ABC的面积为6求点C的坐标;20. 某报社为调查湖州市民对大范围雾霾天气的成因、影响以及应对措施的了解程度,做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题.对雾霾的了解程度 百分比 A 非常了解 5% B 比较了解 m% C 基本了解 45% D 了解 n%
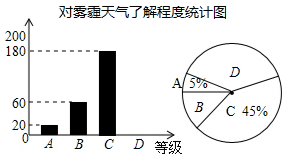 (1)、本次参与调查的市民共有人,m= , n=;(2)、图 2所示的扇形统计图中 D部分扇形所对应的圆心角是度;(3)、根据调查结果.学校准备开展关于雾霾知识竞赛,某班要从小明和小刚中选一人参加,现设计了如下游戏来确定:在一个不透明的袋中装有 2个红球和 3个白球,它们除了颜色外都相同,小明先从袋中随机摸出一个球,小刚再从剩下的四个球中随机摸出一个球,若摸出的两个球颜色相同,则小明去;否则小刚去.现在,小明同学摸出了一个白球,则小明参加竞赛的概率为多少?21. 如图,AB是⊙O的直径,BC⊥AB,弦AD∥OC。
(1)、本次参与调查的市民共有人,m= , n=;(2)、图 2所示的扇形统计图中 D部分扇形所对应的圆心角是度;(3)、根据调查结果.学校准备开展关于雾霾知识竞赛,某班要从小明和小刚中选一人参加,现设计了如下游戏来确定:在一个不透明的袋中装有 2个红球和 3个白球,它们除了颜色外都相同,小明先从袋中随机摸出一个球,小刚再从剩下的四个球中随机摸出一个球,若摸出的两个球颜色相同,则小明去;否则小刚去.现在,小明同学摸出了一个白球,则小明参加竞赛的概率为多少?21. 如图,AB是⊙O的直径,BC⊥AB,弦AD∥OC。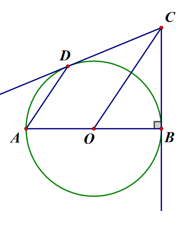 (1)、求证:DC是⊙O的切线(2)、已知AB=6,CB=4,求线段AD的长22. 某工厂上班高峰期员工到达单位的累积人数y随时间x的变化情况如图所示,已知前10分钟,y可看作是x的二次函数,并在10分钟时,累计到达人数为最大值500人,10分钟之后员工全部到岗,累计人数不变。回答下列问题:
(1)、求证:DC是⊙O的切线(2)、已知AB=6,CB=4,求线段AD的长22. 某工厂上班高峰期员工到达单位的累积人数y随时间x的变化情况如图所示,已知前10分钟,y可看作是x的二次函数,并在10分钟时,累计到达人数为最大值500人,10分钟之后员工全部到岗,累计人数不变。回答下列问题: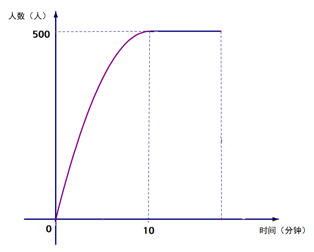 (1)、求出0-10分钟内,y与x之间的函数解析式;(2)、受新型冠状病毒影响,员工在进入单位大门时都应该配合监测体温。如果员工一到达工厂大门就开始接受体温测量,工厂大门口有体温检测岗位2个,每个岗位的工作人员每分钟检测10人,问:工厂门口等待接受体温测量的队伍最多时有多少人;(3)、在(1)(2)的前提下,员工检测体温到第5分钟时,为提高通过效率,减缓拥堵情况,如果要在接下来的10分钟内让全部到达等待的员工都能完成体温检测,问:此时需至少增设几个体温检测岗位?23. 如图(1)、【问题探究】
(1)、求出0-10分钟内,y与x之间的函数解析式;(2)、受新型冠状病毒影响,员工在进入单位大门时都应该配合监测体温。如果员工一到达工厂大门就开始接受体温测量,工厂大门口有体温检测岗位2个,每个岗位的工作人员每分钟检测10人,问:工厂门口等待接受体温测量的队伍最多时有多少人;(3)、在(1)(2)的前提下,员工检测体温到第5分钟时,为提高通过效率,减缓拥堵情况,如果要在接下来的10分钟内让全部到达等待的员工都能完成体温检测,问:此时需至少增设几个体温检测岗位?23. 如图(1)、【问题探究】如图1,锐角△ABC中,分别以AB、AC为边向外作等腰直角△ABE和等腰直角△ACD,使AE=AB,AD=AC,∠BAE=∠CAD=90°,连接BD,CE,试猜想BD与CE的大小关系,不需要证明.
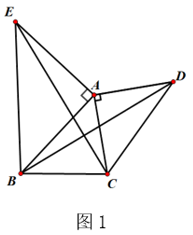 (2)、【深入探究】
(2)、【深入探究】如图2,锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD、CE,试猜想BD与CE的大小关系,并说明理由.
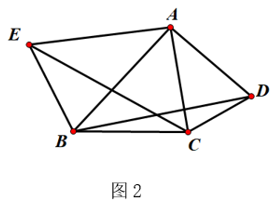 (3)、【拓展应用】
(3)、【拓展应用】如图3,在△ABC中,∠ACB=45°,以AB为直角边,A为直角顶点向外作等腰直角△ABD,连接CD,若AC= ,BC=3,则CD长为.
 (4)、如图4,已知在平面直角坐标系xOy中,O为坐标原点,A(0, )、P(3,0),过点P作直线l⊥x轴,点B是直线l上的一个动点,线段AB绕点A按逆时针方向旋转30°得到线段AC.则AC+PC的最小值为 .
(4)、如图4,已知在平面直角坐标系xOy中,O为坐标原点,A(0, )、P(3,0),过点P作直线l⊥x轴,点B是直线l上的一个动点,线段AB绕点A按逆时针方向旋转30°得到线段AC.则AC+PC的最小值为 .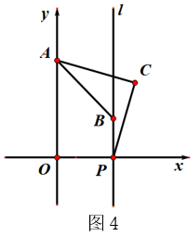 24. 在平面直角坐标系中,抛物线C外: , 抛物线C内 : 的对称轴为直线 ,且C内的图象经过点A(- 3,- 2),动直线 与抛物线C内 交于点M,与抛物线C外 交于点N。
24. 在平面直角坐标系中,抛物线C外: , 抛物线C内 : 的对称轴为直线 ,且C内的图象经过点A(- 3,- 2),动直线 与抛物线C内 交于点M,与抛物线C外 交于点N。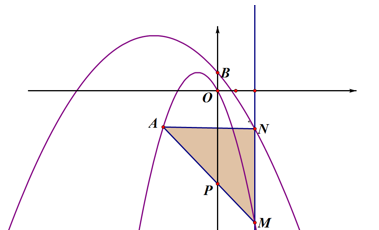 (1)、求抛物线C内的表达式;(2)、当△AMN是以MN为直角边的等腰直角三角形时,求 的值;(3)、在(2)的条件下,设抛物线C外与y轴交于点B,连结AM交y轴于点P,连结PN。
(1)、求抛物线C内的表达式;(2)、当△AMN是以MN为直角边的等腰直角三角形时,求 的值;(3)、在(2)的条件下,设抛物线C外与y轴交于点B,连结AM交y轴于点P,连结PN。①在P点上方的y轴上是否存在点K,使得∠KNP=∠ONB?若存在,求出点K的坐标,若不存在,说明理由。
②若平面内有一点G,且PG=1,是否存在这样的点G,使得∠GNP=∠ONB?若存在,直接写出点G的坐标,若不存在,说明理由。