江苏省常熟市外国语初中2020-2021学年八年级上学期数学9月月考试卷
试卷更新日期：2020-11-11 类型：月考试卷
一、单选题
-
1. 下列四个图案中，不是轴对称图案的是（ ）A、
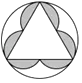B、
C、
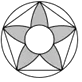D、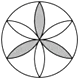
2. 已知等腰三角形两边的长分别为3和7，则此等腰三角形的周长为（ ）A、13 B、17 C、13或17 D、13或103. 下列说法中，正确的是（ ）A、 =±5 B、 =﹣3 C、± =±6 D、 =﹣104. 到三角形三个顶点距离相等的点是（ ）A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点5. 下列各组数作为三角形的边长，其中不能构成直角三角形的是（ ）A、6，8，10 B、5，12，13 C、9，40，41 D、7，9，126. 如图，在△ABC中，AB=AC，∠C=65°，AB的垂直平分线MN交于AC于D点，则∠DBC的度数是 （ ）
A、15° B、20° C、25° D、30°7. 如图，△ABC 中，AB=AC，AD 是∠BAC 的平分线，已知 AB=5，AD=3，则 BC的长为（ ）
A、5 B、4 C、10 D、88. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离 为0.7米，梯子顶端到地面的距离 为2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端到地面的距离 为1.5米，则小巷的宽为（ ）
A、2.5米 B、2.6米 C、2.7米 D、2.8米9. 如图“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D、E可在槽中滑动，若∠BDE=72°，则∠CDE的度数是（ ）
A、63° B、65° C、75° D、84°10. 如图，在RtΔABC中，∠ACB＝90°，AC=9，BC=12，AD是∠BAC的平分线，若点P，Q分别是AD和AC上的动点，则PC＋PQ的最小值是（ ）
A、 B、 C、12 D、15二、填空题
-
11. 计算：= ．
12. 已知等腰三角形的一个内角为 50°，则顶角为.13. 若某个正数的两个平方根分别是2a﹣1与2a+5，则a=.14. 已知一直角三角形的两边分别为3和4，则第三边长的平方是；15. 如图，在Rt△ABC中，∠ACB=90°，BC=6，AC=8，分别以点A，B为圆心，大于线段AB长度一半的长为半径作弧，相交于点E，F，过点E，F作直线EF，交AB于点D，连结CD，则CD的长是 ．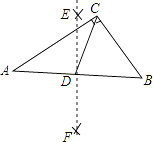
16. 如图，在△ABC中，ED BC，∠ABC和∠ACB的平分线分别交ED于点G、F，若BE=6，DC=8， DE=20，则FG=.
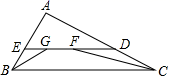17. 如图，在RtΔABC中，∠C=90º， BC=6cm， AC=8cm，如果按图中所示方法将ΔBCD沿BD折叠，使点C落在边AB上的点C'处，那么ΔADC'的周长是cm.
18. 如图△ABC 中，AC=BC，∠ACB=120°，点 D 在线段 AB 上运动（D 不与 A、B 重合），连接 CD，作∠CDE=30°，DE 交 BC 于点 E，若△CDE 是等腰三角形，则∠ADC 的度数是.
三、解答题
-
19. 求下列各式中x的取值(1)、2x2-8 =0(2)、4（2x-1）2 =920. 已知2a－1的算术平方根为3，3a+b－1的算术平方根为4，求a+2b的平方根.21. 如图，在边长为1个单位长度的小正方形组成的网格中，点A、B、C在小正方形的顶点上.
(1)、 的面积为；（请写出作答步骤）(2)、在图中画出 与 关于直线l成轴对称的；(3)、在直线l上找一点P，使PA+PB的长最短，则这个最短长度的平方为.22. 已知：在Rt△ABC中，∠A=90°.
(1)、利用圆规和直尺，在图中找一个点P，使点P到AB，AC的距离相等，且PB= PC.（不写作法，保留作图痕迹）(2)、若BC的垂直平分线交直线AB于点E，AC=12，AE=5，求AB的长.23.如图，在△ABC中，AB=AC，点D是BC边上的中点，DE、DF分别垂直AB、AC于点E和F．
求证：DE=DF．
24. 如图，已知CD=3cm，AD=4cm，∠ADC=90°，BC=12cm，AB=13cm，求阴影部分的面积.
25. 如图，在吴中区上方山动物园里有两只猴子在一棵树CD上的点B 处，且BC=5m，它们都要到池塘A处吃东西，其中一只猴子甲沿树爬至C再沿CA 走到离树24m处的池塘A处，另一只猴子乙先爬到树顶D处后再沿缆绳DA线段滑到A处.已知猴子甲所经过的路程比猴子乙所经过的路程多2m，设BD为xm.
(1)、请用含有x的整式表示线段AD的长为m；(2)、求这棵树高有多少米？26. 如图，在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG⊥CE于G， CD=AE.
(1)、求证： CG=EG.(2)、已知BC=13， CD=5，连结ED，求△EDC 的面积.27. 如图1，已知△ABC和△EFC都是等边三角形，且点E在线段AB上.
(1)、求证：BF∥AC；(2)、过点E作EG∥BC交AC于点G，试判断△AEG的形状并说明理由；(3)、如图2，若点D在射线CA上，且ED＝EC，求证：AB＝AD＋BF.28. 如图1，△ABC中，CD⊥AB于D，且BD：AD：CD=2：3：4，
(1)、试说明△ABC是等腰三角形；(2)、已知 ，动点M从点B出发以每秒lcm的速度沿线段BA向点A运动，同时动点N从点A出发以相同速度沿线段AC向点C运动，当其中一点到达终点时整个运动都停止，设点M运动的时间为t（秒），若点E是边AC的中点，问在点M运动的过程中，△MDE能否成为等腰三角形？若能，求出t的值：若不能，请说明理由.