重庆市巴南区七校共同体2020-2021学年八年级上学期数学第一次月考试卷
试卷更新日期：2020-11-11 类型：月考试卷
一、单选题
-
1. 下列线段长能构成三角形的是（ ）A、3、4、8 B、2、3、6 C、5、6、11 D、5、6、102. 王师傅用4根木条钉成一个四边形木架，如图．要使这个木架不变形，他至少还要再钉上几根木条？（ ）
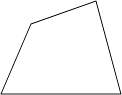A、0根 B、1根 C、2根 D、3根3. 如图，某同学把一块三角形的玻璃打碎成了三块，现在他要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带（ ）去.
A、①和② B、②和③ C、①和③ D、②4. 如图，在 中，AC边上的高是（ ）
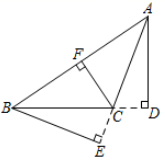A、BE B、AD C、CF D、AF5. 若一个多边形的每一个外角都是45°，则这个多边形的内角和是（ ）.A、540° B、720° C、1080° D、1260°.6. 如图，已知 ，那么添加下列一个条件后，仍无法判定 的是（ ）
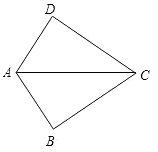A、 B、 C、 D、7. 将一个三角形纸片剪开分成两个三角形，这两个三角形不可能（ ）A、都是锐角三角形 B、都是直角三角形 C、都是钝角三角形 D、是一个锐角三角形和一个钝角三角形8. 具备下列条件的△ABC中，不是直角三角形的是（ ）A、∠A＝∠B＝3∠C B、∠A﹣∠B＝∠C C、∠A+∠B＝∠C D、∠A：∠B：∠C＝1：2：39. 已知在ΔABC中，AB=AC，周长为24，AC边上的中线BD把ΔABC分成周长差为6的两个三角形，则ΔABC各边的长分别为
A、10、10、4 B、6、6、12 C、4、5、10 D、以上都不对10. 在ΔABC中，BD 为 AC边上的高，∠ABD＝30°， ∠BAC的度数为（ ）.A、60° B、65° C、125° D、60°或120°11. 如图△ABC中，∠A=96°，延长BC到D，∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2 ， 依此类推，∠A4BC与∠A4CD的平分线相交于点A5 ， 则∠A5的度数为（ ）
A、19.2° B、8° C、6° D、3°12. 如图，在ΔABC中，DE⊥BC，垂足为D，且BD＝DC，BF平分∠ABC，交CE于F.若BE=AC，∠ACE=12°，则∠EFB的度数为（ ）.
A、58 B、63 C、67 D、70二、填空题
-
13. 等腰三角形的两边长分别是3和7，则其周长为 ．14. 如图，已知 于点P， ，请增加一个条件，使 ≌ 不能添加辅助线 ，你增加的条件是.
15. 在ΔABC中，∠C=90°，AD平分∠CAB，交BC与D，过点D作DE⊥AB于E，BC=8cm，BD=5cm，DE=.
16. 如图，在ΔABC中，∠ACB＝90°，点D在AB上，将ΔBDC沿CD折叠，点B落在AC边上的点B′处，若∠ADB′＝20°，则∠A的度数是.
17. 如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，已知EH=EB=3，AE=4，则CH的长是
18. 如图，任意画一个∠BAC＝60°的△ABC，再分别作△ABC的两条角平分线BE和CD，BE和CD相交于点P，连接AP，有以下结论：①∠BPC＝120°；②AP平分∠BAC；③AD＝AE；④PD＝PE；⑤BD+CE＝BC；其中正确的结论为.（填写序号）
三、解答题
-
19. 如图，AD，CE是△ABC的两条高；已知AD＝10，CE＝9，AB＝12.
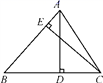(1)、求△ABC的面积；(2)、求BC的长.20. 如图，已知AB＝CD AC=BD.求证：∠BAC＝ ∠BDC.
21. 如图，在 中，∠ACB＝90°，∠A＝38°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)、求∠DBE的度数；(2)、过点D作DF∥BE，交AC的延长线于点F，求∠F的度数.22. 如图，点B，F，C，E在同一条直线上， AC∥DE，AC＝DE，∠A＝∠D.
(1)、求证：AB∥DF；23. 如图，AB＝AC，AD＝AE，∠BAC＝∠DAE.
(1)、求证：△ABD≌△ACE；(2)、若∠1＝25°，∠2＝30°，求∠3的度数.24. 已知：如图， ABC中，AB=BC，CD⊥AB于点D，BE⊥AC于点E，BE与CD相交于点O.
(1)、求证：AE=EC；(2)、在线段AB上取一点N，使ON=OC，过O作OM⏊BC，垂足为M，若BN=4，BC=10，求CM的长.25.
(1)、问题背景：如图 1，在四边形 ABCD 中，AB = AD，∠BAD= 120°，∠B =∠ADC= 90°，E，F 分别是 BC， CD 上的点，且∠EAF = 60°，探究图中线段BE，EF，FD之间的数量关系.
小明同学探究此问题的方法是延长FD到点G，使DG=BE， 连结AG，先证明Δ ΔADG，再证明Δ ΔAGF，可得出结论，他的结论应是.
(2)、探索延伸：如图 2，在四边形ABCD 中，AB=AD，∠B+∠D=180°，E，F分别是BC，CD上的点，∠EAF= ∠BAD，上述结论是否依然成立？并说明理由.
26. 如图（1），AB＝4 ，AC⊥AB，BD⊥AB，AC＝BD＝3 .点 P 在线段 AB 上以 1 的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为 t（s）.
(1)、若点 Q 的运动速度与点 P 的运动速度相等，当 ＝1 时，△ACP 与△BPQ 是否全等，请说明理由， 并判断此时线段 PC 和线段 PQ 的位置关系；(2)、如图（2），将图（1）中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其他条件不变.设点 Q 的运动速度为 ，是否存在实数x，使得△ACP 与△BPQ 全等？若存在，求出相应的x、t的值；若不存在，请说明理由.