江苏省连云港市灌云县西片2020-2021学年八年级上学期数学第一次月考试卷
试卷更新日期：2020-11-11 类型：月考试卷
一、选择题
-
1. 下列图形中不是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列说法正确的是（ ）A、全等三角形是指形状相同的两个三角形 B、全等三角形是指面积相等的两个三角形 C、两个等边三角形是全等三角形 D、全等三角形是指两个能完全重合的三角形3. 如图，已知△ABC≌△BAD，A与B，C与D分别是对应顶点，若AB＝3cm，BC＝2cm，AC＝4cm，则AD的长为（ ）
A、2cm B、3cm C、4cm D、不能确定4. 如图，某同学不小心把一块三角形玻璃打碎成三块，现在要到玻璃店配一块与原来完全相同的玻璃，最省事的方法是( )
A、带①和②去 B、只带②去 C、只带③去 D、都带去5. 下列条件能判定△ABC≌△DEF的一组是（ ）A、∠A＝∠D，∠B＝∠E，∠C＝∠F B、AB＝DE，BC＝EF，∠A＝∠D C、∠A＝∠D，∠C＝∠F，AC＝DF D、△ABC的周长等于△DEF的周长6. 如图，将一张长方形纸片ABCD沿AE折叠，若∠BAD′＝28°，则∠AED′等于（ ）
A、28° B、59° C、66° D、68°7. 已知：如图，在△ABC中，∠C＝63°，AD是BC边上的高，CD＝FD，点E在AC上，BE交AD于点F，BF＝AC，则∠ABF的度数为（ ）
A、18° B、36° C、48° D、63°8. 如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE，下列说法：①△ABD 和△ACD面积相等；②∠BAD＝∠CAD；③△BDF≌△CDE；④BF∥CE；⑤CE＝AE，其中正确的是（ ）
A、①② B、③⑤ C、①③④ D、①④⑤二、填空题
-
9. 如图，已知△ABC的六个元素，其中a、b、c表示三角形三边的长，则下面甲、乙、丙三个三角形中和△ABC一定全等的图形是.
10. 黑体汉字中的“中”“田”“日”等都是轴对称图形，请至少再写出三个具有这种特征的汉字：.11. 如图，AC⊥BC，AD⊥BD，垂足分别是C、D，若要用“HL”得到Rt△ABC≌Rt△BAD，则你添加的条件是.（写一种即可）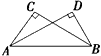
12. 如图，AD、BC表示两根长度相同的木条，若O是AD、BC的中点，经测量AB＝9cm，则容器的内径CD为 cm.
13. 如图，在正方形网格中有两个小正方形被涂黑，再涂黑一个图中其余的小正方形，使得整个被涂黑的图案构成一个轴对称图形，那么涂法共有种.
14. 如图所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=20°，∠2=25°，则∠3=.
15. 如图所示， 内一点P， ， 分别是P关于OA，OB的对称点， 交OA于点M，交OB于点N，若 ，则 的周长是.
16. 如图1是个轴对称图形，且每个角都是直角，长度如图所示，小王按照如图2所示的方法玩拼图游戏，两两相扣，相互不留空隙，那么小王用2020个这样的图形（图1）拼出来的图形的总长度是.（结果用m，n表示）
三、解答题
-
17. 沿着图中的虚线，用四种不同的方法将下面的图形分成两个全等的图形
18. 已知：AB＝AC ， BE＝CD ．
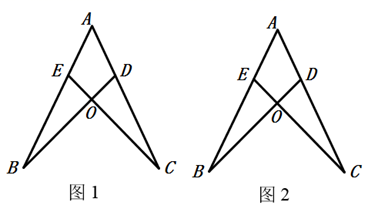(1)、如图1，求证：∠B＝∠C；(2)、如图2，连接AO ， 不添加任何辅助线，直接写出图中所有的全等三角形．19. 如图，AB//CD，∠B＝∠D，O是CD的中点，连接AO并延长，交BC的延长线于点E.
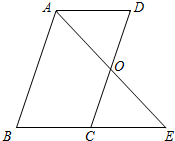(1)、试判断AD与BE有怎样的位置关系，并说明理由；(2)、试说明△AOD≌△EOC.20. 某段河流的两岸是平行的，数学兴趣小组在老师带领下不用涉水过河就测得的宽度，他们是这样做的：①在河流的一条岸边B点，选对岸正对的一棵树A；②沿河岸直走20m有一棵树C，继续前行20m到达D处；③从D处沿河岸垂直的方向行走，当到达A树正好被C树遮挡住的E处停止行走；④测得DE的长为5米.
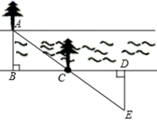(1)、河的宽度是米.(2)、请你说明他们做法的正确性.21. 已知如下图，求作△ABC关于对称轴l的轴对称图形△A′B′C′.
22. 如图，以 为对称轴，画出下面图形的对称图形，观察这个图形和它的轴对称图形构成什么三角形，根据你所学习的轴对称图形的基本特征，结合你所画的图形写出两个正确结论.
23. 如图，在△ABC中，AC＝BC，直线l经过顶点C，过A，B两点分别作l的垂线AE，BF，E，F为垂足.AE＝CF，求证：∠ACB＝90°.
24. 如图，在△ABC中，直线l交AB于点M，交BC于点N，点B关于直线l的对称点D在线段BC上，且AD⊥MD，∠B=28°，求∠DAB的度数．
25. 在 中，AB=AC，D是直线BC上一点，以AD为一条边在AD的右侧作 ，使 AE=AD ，∠DAE=∠BAC ，连接CE.
(1)、如图，当点D在BC延长线上移动时，若 ，则 .(2)、设 ， .①当点D在BC延长线上移动时， 与 之间有什么数量关系？请说明理由；
②当点D在直线BC上 不与B，C两点重合 移动时， 与 之间有什么数量关系？请直接写出你的结论.
26. 如图，在△ABC中，AB=AC=8，BC=12，点D从B出发以每秒2个单位的速度在线段BC上从过点B向点C运动，点E同时从点C出发，以每秒2个单位的速度在线段AC上从点A运动，连接AD、DE，设D、E两点运动时间为 秒.
(1)、运动秒时，CD=3AE.(2)、运动多少秒时，△ABD≌△DCE能成立，并说明理由；(3)、若△ABD≌△DCE，∠BAC= 则∠ADE=(用含 的式子表示).