江苏省江阴市青阳片2020-2021学年八年级上学期数学10月月考试卷
试卷更新日期：2020-11-11 类型：月考试卷
一、选择题
-
1. 下列美丽的图案中是轴对称图形的个数有（ ）
A、1个 B、2个 C、3个 D、4个2. 一张菱形纸片按图1－1、图1－2依次对折后，再按图1－3打出一个圆形小孔，则展开铺平后的图案（ ）
A、
B、
C、
D、
3. 用直尺和圆规作一个角等于已知角，如图，能得出∠A′O′B′=∠AOB的依据是（ ）.
A、SAS B、AAS C、ASA D、 SSS4. 如图，在△ABC中，BC=8cm，AB的垂直平分线交AB于点D，交边AC于点E，△BCE的周长等于18cm，则AC的长等于（ ）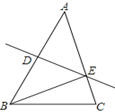
A、8cm B、10cm C、12cm D、14cm5. △ABC是格点三角形（顶点在网格线的交点），则在图中能够作出△ABC全等且有一条公共边的格点三角形（不含△ABC）的个数是（ ）
A、1个 B、2个 C、3个 D、4个6. 到三角形三个顶点距离相等的点是（ ）A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点7. 如图OP平分∠AOB，PC⊥OA于C，D在OB上，PC=3，则PD的大小关系是（ ）
A、PD≥3 B、PD=3 C、PD≤3 D、不能确定8. 如图，点B，F，C，E在一条直线上，FB=CE，AC=DF，能从下列三个条件： ①AB=DE； ②∠A=∠D；③∠ACB=∠DFE中选择一个合适的条件，使AB∥ED成立的个数是（ ）
A、0个 B、1个 C、2个 D、3个9. 如图，在△ABC中AD是∠A的外角平分线，P是AD上一动点且不与点A，D重合，记PB＋PC＝a，AB＋AC＝b，则a、b的大小关系是（ ）
A、a＞b B、a＝b C、a＜b D、不能确定10. 如图所示，△ABE和△ADC是△ABC分别沿着AB，AC边翻折180°形成的，若∠1：∠2：∠3=13：3：2，则∠α的度数为（ ）
A、80° B、100° C、90° D、50°二、填空题
-
11. 在等边三角形、正方形、圆、直角三角形中，对称轴最多的图形是.12. 如图，从镜子中看到一钟表为2：30，此时的实际时刻是.
13. 如图，已知AB∥CF，E为DF的中点，若AB=10cm，CF=6cm，则BD=cm.
14. 如图，若△OAD≌△OBC，且∠O=75o ， ∠C=10o ， 则∠OAD=°.
15. 如图将一张长方形纸片沿EF折叠后，点A、B分别落在A′、B′的位置，如果∠2=70°，则∠1的度数是.
16. 如图，∠MON内有一点P，P点关于OM的轴对称点是G，P点关于ON的轴对称点是H， GH分别交OM、ON于A、B点，若 ，则 .
17. AD是△ABC的边BC上的中线，AB=5，AD=4，则AC的取值范围是.18. 如图，Rt△ABC中，∠ACB＝90º，AC＝5，BC＝12，AB=13，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段EF的长为.
三、解答题
-
19. 如图，在所给网格图（每小格均为边长是1的正方形）中完成下各题：（用直尺画图）
(1)、画出格点△ABC（顶点均在格点上）关于直线DE对称的△A1B1C1；(2)、在DE上画出点P，使PB＋PC最小；(3)、在DE上画出点Q，使QA=QC.20. 尺规作图：某学校正在进行校园环境的改造工程设计，准备在校内一块四边形花坛内栽上一棵桂花树.如图，要求桂花树的位置点P，到花坛的两边AB，BC的距离相等，并且点P到点A，D的距离也相等.请用尺规作图作出栽种桂花树的位置点P（不写作法，保留作图痕迹）.
21. 如图，在△AOD和△BOC中，AB与CD相交于点O，AO=BO，CO=DO.
求证：
(1)、△AOD≌△BOC；(2)、AD∥BC.22. 如图，DE⊥AB于E，DF⊥AC于F，若BD=CD、BE=CF.
(1)、求证：AD平分∠BAC；(2)、已知AC=18， BE=4，求AB的长.23. 已知：如图∠BAC的角平分线与BC的垂直平分线DG交于点D，DE⊥AB，DF⊥AC，垂足分别为E，F.
(1)、说明：BE=CF；(2)、若AF=6，△ABC的周长为20，求BC的长.24. 如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．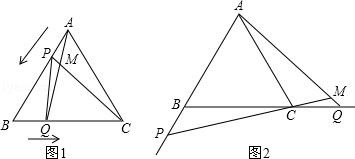
(1)、求证：△ABQ≌△CAP；(2)、当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．(3)、如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，则求出它的度数．25. 如图，在△ABC中，AB=AC=10cm；BC=6cm，点D为AB的中点.
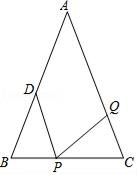(1)、如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动.①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
(2)、若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B出发都逆时针沿△ABC三边运动，直接写出经过多少秒后，点P与点Q第一次在△ABC的那一条边上相遇.