江苏省东台市第四联盟2020-2021学年八年级上学期数学第一次月考试卷

试卷更新日期：2020-11-11 类型：月考试卷

进入出卷网下载

一、选择题

1. 下面是我国部分汽车标志图形，其中不是轴对称图形是（）

A、 B、 C、 D、

查看试题解析
2. 下列语句：①全等三角形的面积相等；②周长相等的三角形是全等三角形；③成轴对称的两个图形全等；④全等的两个三角形成轴对称.其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 已知图中的两个三角形全等，则∠α的度数是（）

A、72° B、60° C、58° D、50°

查看试题解析
4. 在锐角三角形ABC内一点P,，满足PA=PB=PC,则点P是△ABC （）

A、三条角平分线的交点 B、三条中线的交点 C、三条高的交点 D、三边垂直平分线的交点

查看试题解析
5. 如图，已知 $A B = A D$ ，那么添加下列一个条件后，仍无法判定 $Δ A B C ≌ Δ A D C$ 的是（）

A、 $C B = C D$ B、 $∠ B A C = ∠ D A C$ C、 $∠ B C A = ∠ D C A$ D、 $∠ B = ∠ D = 90 °$

查看试题解析
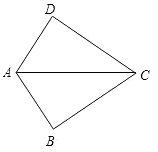6. 如图， $△ A B C$ 的周长为20cm，把 $△ A B C$ 沿DE翻折，使点C和点A重合，若AE=3cm，则 $△ A B D$ 的周长是（）

A、14cm B、15cm C、16cm D、17cm

查看试题解析
7. 如图，∠E=∠F=90°，∠B=∠C，AE=AF，给出下列结论：①∠1=∠2；②BE=CF；③ $△ B D N ≌ △ C D M$ ；④CD=AE.其中不正确的结论有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 如图， $△ A B C$ 的面积为8cm² ， AP垂直∠B的平分线BP于P，若 $△ A B P$ 的面积为3，则 $△ A C P$ 的面积为（）

A、1cm² B、2cm² C、3cm² D、4cm²

查看试题解析

二、填空题

9. 小强站在镜前，从镜子中看到镜子对面墙上挂着的电子表，其读数如图所示，则电子表的实际时刻是.

查看试题解析
10. 如图，∠1＝∠2，要使△ABE≌△ACE，还需添加一个条件是.（填上一个条件即可）

查看试题解析
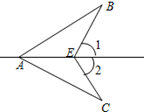11. 如图，已知AB⊥CD，垂足为B，且 $△ A B C ≌ △ D B E$ ，BC=4，BD=6，则AE=.

查看试题解析
12. 如图， $△ A B C$ 按顺时针方向转动40°得 $△ A E D$ ，点D恰好在边BC上，则∠C＝°.

查看试题解析
13. 如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=

查看试题解析
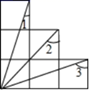14. 如图，在△ABC中，分别以点A和点B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD.若△ADC的周长为10，AB=8，则△ABC的周长为.

查看试题解析
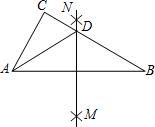15. 已知有两个三角形全等，若一个三角形三边的长分别为3、5、7，另一个三角形三边的长分别为3、3a﹣2b、a+2b ，则a+b＝．

查看试题解析
16. 如图， $△ A B E$ 和 $△ A D C$ 是 $△ A B C$ 分别沿着AB、AC边翻折180°形成的，若∠1：∠2：∠3=7：2：1，则∠α的度数为°.

查看试题解析
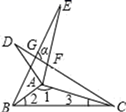17. 如图，CA⊥AB，垂足为点A，AB=12，AC=6，射线BM⊥AB，垂足为点B，一动点E从A点出发以2厘米/秒沿射线AN运动，点D为射线BM上一动点，随着E点运动而运动，且始终保持ED=CB，当点E经过秒时，△DEB与△BCA全等.

查看试题解析
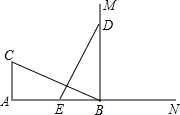18. 如图，在 $△ A B C$ 中，AB=AC=10，BC=12，AD=8，AD⊥BC.若P、Q分别是AD和AC上的动点，则PC+PQ的最小值是.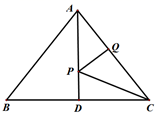

查看试题解析

三、解答题

19. 如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上.

（ 1 ）在图中画出与△ABC关于直线l成轴对称的△A′B′C′；

（ 2 ）在直线l上找一点P，使PB+PC的长最短.

查看试题解析
20. 如图，在 $△ A B C$ 和 $△ A B D$ 中，AC与BD相交于点E，AD=BC，AC=BD.求证：∠C=∠D.

查看试题解析
21. 如图，已知AD是 $△ A B C$ 的中线，过点B作BE⊥AD，垂足为E.若BE=6，求点C到AD的距离.

查看试题解析
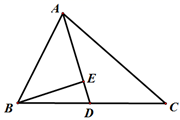22. 如图，在 $△ A B C$ 中∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.

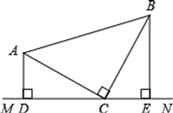(1)、求证： $△ A D C ≌ △ C E B$ ；

(2)、若AD=2，BE=3，求 $△ A B C$ 的面积.

查看试题解析
23. 如图，在 $△ A B C$ 中，边AB，AC的垂直平分线相交于点O，分别交BC与D、E.

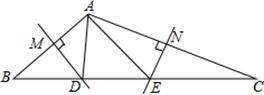(1)、若∠BAC=120°，则∠DAE=.

(2)、连接OA、OB、OC， $△ A D E$ 的周长为6cm， $△ B O C$ 的周长为14cm，求OA的长.

查看试题解析
24. 在 $△ A B C$ 中，AB=AC，点D是直线BC上一点(不与B、C重合)，以AD为一边在AD的右侧作 $△ A D E$ ，使AD=AE，∠DAE=∠BAC，连接CE

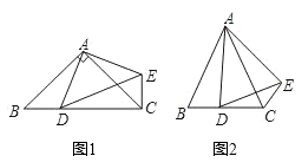(1)、如图1，当点D在线段BC上，且∠BAC=90°.
①说明： $△ A B D ≌ △ A C E$ ；

②线段CE、CD、BC的数量关系为_▲_.

(2)、如图2，当点D在直线BC上，设∠BAC=α，∠BCE=β.则α，β之间有怎样的数量关系？请直接写出你的结论.

查看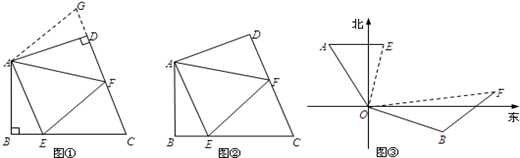试题解析
25.

(1)、如图①，四边形ABCD中，AB=AD，∠B=∠ADC=90°.E，F分别是BC，CD上的点，且BE+FD=EF.试探究图中∠EAF与∠BAD之间的数量关系.小明同学探究此问题的方法是：延长FD到G，使DG=BE，连结AG.先证明 $△ A B E ≌ △ A D G$ ，再证明 $△ A E F ≌ △ A G F$ ，从而得出∠EAF=∠GAF，最后得出∠EAF与∠BAD之间的数量关系是.

(2)、将（1）中的条件“∠B=∠ADC=90°”改为“∠B+∠D=180°”（如图②），其余条件不变，上述数量关系是否成立，成立，请证明；不成立，说明理由

(3)、如图③，中俄两国海军在南海举行联合军事演习，中国舰艇在指挥中心（O）北偏西30°的A处，俄罗斯舰艇在指挥中心南偏东70°的B处，两舰艇到指挥中心距离相等.接到行动指令后，中国舰艇向正东方向以60海里/小时的速度前进，俄罗斯舰艇沿北偏东50°的方向以80海里/小时的速度前进，2小时后，指挥中心观测到两舰艇分别到达E，F处且相距280海里.求此时两舰艇的位置与指挥中心（O处）形成的夹角∠EOF的大小.

查看试题解析