天津市西青区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-10 类型:期末考试
一、单选题
-
1. 下列各式从左到右的变形属于因式分解的是( )A、 B、( x + 1) ( x - 1) = - 1 C、 + a - 5 = (a - 2 ) (a + 3 ) + 1 D、 y + x = xy ( x + y )2. 下列计算结果正确的是( )A、a12÷a3= a4 B、(3 )3= 9 C、( a-b )2=a2-ab+b 2 D、2a∙3a = 63. 若分式 的值为0,则x的值为( )A、3 B、-3 C、3或-3 D、04. 我们用肥皂水吹泡泡,泡沫的厚度约为 0.000326 毫米,0.000326用科学记数法表示为( )A、3.26 ´ 10-4 B、0.326 ´ 10-4 C、3.26 ´10-5 D、32.6 ´ 10-45. 四边形 ABCD 中,如果 ∠A + ∠C + ∠D = 280° ,则 ∠B 的度数是( )A、20° B、80° C、90° D、170°6. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
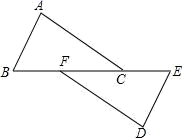
D、 7. 如果△ABC≌△DEF,且△ABC的周长为100 cm,A,B分别与D,E对应,AB=30 cm,DF=25 cm,则BC的长为( )A、45 cm B、55 cm C、30 cm D、25 cm8. 已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )A、1 B、2 C、8 D、119. 若 ,则 的值为( )A、 B、-2 C、 D、10. 已知(m-n)2=8,(m+n)2=2,则m2+n2=( )A、10 B、6 C、5 D、311. 如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
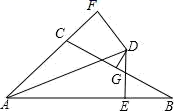
7. 如果△ABC≌△DEF,且△ABC的周长为100 cm,A,B分别与D,E对应,AB=30 cm,DF=25 cm,则BC的长为( )A、45 cm B、55 cm C、30 cm D、25 cm8. 已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )A、1 B、2 C、8 D、119. 若 ,则 的值为( )A、 B、-2 C、 D、10. 已知(m-n)2=8,(m+n)2=2,则m2+n2=( )A、10 B、6 C、5 D、311. 如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )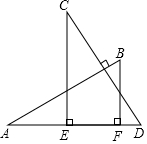 A、 B、 C、 D、12. 如图,在 △ABC 中,ED∥BC , ∠ABC 和∠ACB 的平分线分别交 ED 于点 G 、F , 若 FG = 2 ,ED = 6 ,则EB + DC 的值为( )
A、 B、 C、 D、12. 如图,在 △ABC 中,ED∥BC , ∠ABC 和∠ACB 的平分线分别交 ED 于点 G 、F , 若 FG = 2 ,ED = 6 ,则EB + DC 的值为( )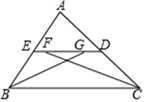 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9二、解答题
-
13. 计算 =14. 等边△ABC 的边长为 4,AD 是 BC 边上的中线,F 是边 AD 上的动点,E 是边 AC 上的点, 当 AE=2,且 EF+CF 取得最小值时.
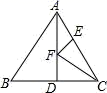 (1)、能否求出∠ECF 的度数?(用“能”或“否”填空);(2)、如果能,请你在图中作出点 F(保留作图痕迹,不写证明).并直接写出∠ECF 的度 数;如果不能,请说明理由.15.(1)、分解因式: .(2)、先化简,再求值:(3x -1)(3x + 1)-(x +3)(9x -6).其中 x =- .16.(1)、计算: ;(2)、先化简,再求值: ,其中 x = -3 .17. 如图,AD 是 △ABC 的高,BE 平分∠ABC 交 AD 于点 E . 若∠C = 76° ,∠BED = 64° .求∠BAC 的度数.
(1)、能否求出∠ECF 的度数?(用“能”或“否”填空);(2)、如果能,请你在图中作出点 F(保留作图痕迹,不写证明).并直接写出∠ECF 的度 数;如果不能,请说明理由.15.(1)、分解因式: .(2)、先化简,再求值:(3x -1)(3x + 1)-(x +3)(9x -6).其中 x =- .16.(1)、计算: ;(2)、先化简,再求值: ,其中 x = -3 .17. 如图,AD 是 △ABC 的高,BE 平分∠ABC 交 AD 于点 E . 若∠C = 76° ,∠BED = 64° .求∠BAC 的度数.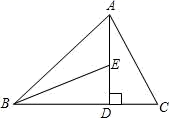 18. 如图,△ABC 在平面直角坐标系中,点 A , B , C 的坐标分别为 A(-2,4),B(4,2),C(2,-1).
18. 如图,△ABC 在平面直角坐标系中,点 A , B , C 的坐标分别为 A(-2,4),B(4,2),C(2,-1).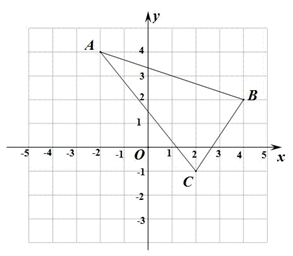 (1)、请在平面直角坐标系内,画出△ABC 关于 x 轴的对称图形△A1B1C1 , 其中,点 A , B , C 的对应点分别为A1 , B1 , C1;(2)、请写出点C(2,-1)关于直线m(直线m上格点的横坐标都为-1)对称的点C2的坐标.19. 注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路,填写表格,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填写表格, 只需按照解答题的一般要求,进行解答即可.
(1)、请在平面直角坐标系内,画出△ABC 关于 x 轴的对称图形△A1B1C1 , 其中,点 A , B , C 的对应点分别为A1 , B1 , C1;(2)、请写出点C(2,-1)关于直线m(直线m上格点的横坐标都为-1)对称的点C2的坐标.19. 注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路,填写表格,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填写表格, 只需按照解答题的一般要求,进行解答即可.某校八年级学生由距博物馆 10km 的学校出发前往参观,一部分同学骑自行车先走,过了20min 后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度 的 2 倍,求骑车同学的速度.
设骑车同学的速度为 xkm / h
(1)、根据题意,利用速度、时间、路程之间的关系,用含有 x 的式子填写下表:速度(千米 / 时)
所用时间(时 )
所走的路程(千米)
骑自行车
x
10
乘汽车
10
(2)、列出方程,并求出问题的解.20. 如图在中 , , , 是 的平分线,交 于点 , 是 的中点,连接 并延长交 的延长线于点 ,连接 .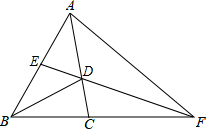
求证:
(1)、 ;(2)、 为等腰三角形21. 在四边形 ABCD 中,E 为 BC 边中点.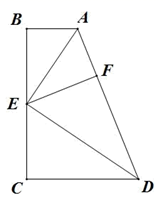 (1)、已知:如图,若 AE 平分∠BAD , ∠AED=90°,点 F 为 AD 上一点,AF=AB.求证:①△ABE≌AFE;
(1)、已知:如图,若 AE 平分∠BAD , ∠AED=90°,点 F 为 AD 上一点,AF=AB.求证:①△ABE≌AFE;②AD=AB+CD
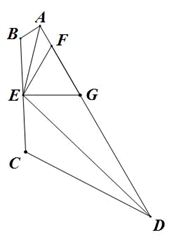
(2)、已知:如图,若 AE 平分∠BAD , DE 平分∠ADC , ∠AED=120°,点 F , G 均为 AD上的点,AF=AB , GD=CD.求证:①△GEF 为等边三角形;
②AD=AB+ BC+CD.
三、填空题