天津市河西区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-10 类型:期末考试
一、单选题
-
1. 计算 的结果是( )A、 B、 C、5 D、2. 下列计算正确的是( )A、a6+a6=a12 B、a6×a2=a8 C、a6÷a2=a3 D、(a6)2=a83. 在一些美术字体中,有的英文字母是轴对称图形. 下面4个字母中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若 ,则 的值为( )A、 B、 C、1 D、5. 如图,点D在AB上,点E在AC上, 与BE相交于点O,且 ,则判定 与 全等的依据是( )
4. 若 ,则 的值为( )A、 B、 C、1 D、5. 如图,点D在AB上,点E在AC上, 与BE相交于点O,且 ,则判定 与 全等的依据是( ) A、 B、 C、 D、6. 请你观察图形,依据图形面积之间的关系,不需要添加辅助线,便可得到一个你非常熟悉的公式,这个公式是( )
A、 B、 C、 D、6. 请你观察图形,依据图形面积之间的关系,不需要添加辅助线,便可得到一个你非常熟悉的公式,这个公式是( ) A、 B、 C、 D、7. 分式方程 的解是( )A、 B、 C、 D、8. 甲从地 到 地要走 小时,乙从 地到 地要走 小时,甲、乙两人分别从 两地同时出发相向而行到相遇需要的时间是( )A、 B、 C、 D、9. 若先化简 ,再求值,且 是满足 的整数,则化简求值的结果为( )A、0或 或-2或4 B、-2或 C、-2 D、10. 如图,在 中, ,以 为圆心,任意长为半径画弧分别交 于点 和 ,再分别以 为圆心,大于 的长为半径画弧,两弧交于点 ,连接 并延长交 于点 ,则下列结论一定成立的个数为( )
A、 B、 C、 D、7. 分式方程 的解是( )A、 B、 C、 D、8. 甲从地 到 地要走 小时,乙从 地到 地要走 小时,甲、乙两人分别从 两地同时出发相向而行到相遇需要的时间是( )A、 B、 C、 D、9. 若先化简 ,再求值,且 是满足 的整数,则化简求值的结果为( )A、0或 或-2或4 B、-2或 C、-2 D、10. 如图,在 中, ,以 为圆心,任意长为半径画弧分别交 于点 和 ,再分别以 为圆心,大于 的长为半径画弧,两弧交于点 ,连接 并延长交 于点 ,则下列结论一定成立的个数为( )
① 是 的平分线;②若 ,则 ;③ ;④点 在 的垂直平分线上.
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 分解因式:3ax2+6axy+3ay2=.12. 计算 的结果等于.13. 一个n边形的内角和为1080°,则n= .14. 如图的三角形纸片中, ,沿过点 的直线折叠这个三角形,使点 落在 边上的点 处,折痕为 ,则 的周长为.
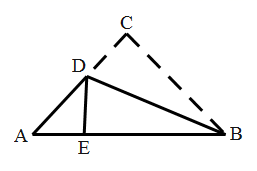 15. 如图,等边 的边长为4, 是 边上的中线, 是 边上的动点, 是 边上一点. 若 ,当 取得最小值时,则 的度数为.
15. 如图,等边 的边长为4, 是 边上的中线, 是 边上的动点, 是 边上一点. 若 ,当 取得最小值时,则 的度数为. 16. 一个容器装有 水,按照如下要求把水倒出:第1次倒出 水,第2次倒出的水是 的 ,第3次倒出的水量是 的 ,第4次倒出的水量是 的 ……第 次倒出的水量是 的 ……按照这种倒水的方法,这 水经 次,倒出的总水量为.
16. 一个容器装有 水,按照如下要求把水倒出:第1次倒出 水,第2次倒出的水是 的 ,第3次倒出的水量是 的 ,第4次倒出的水量是 的 ……第 次倒出的水量是 的 ……按照这种倒水的方法,这 水经 次,倒出的总水量为.三、解答题
-
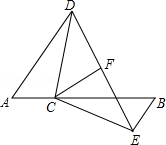
17. 计算:(1)、(2)、18. 解方程 .19. 如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF平分∠DCE.试探索CF与DE的位置关系,并说明理由.
 20. 如图
20. 如图 (1)、如图①,点 在直线 两侧,请你在直线 上画出一点 ,使得 的值最小,简述画法、画出图形;(2)、如图②,点 在直线 同侧,请你在直线 上画出一点 ,使得 的值最小,简述画法并画出示意图.21. 一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?(1)、设江水的流速为 千米/时,填空:轮船顺流航行速度为千米/时,逆流航行速度为千米/时,顺流航行100千米所用时间为小时,逆流航行60千米所用时间为小时.(2)、列出方程,并求出问题的解.22. 在日历上,我们可以发现其中某些数满足一定的规律,如图是2012年8月份的日历. 我们任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交叉相乘,再相减,例如: , ,不难发现,结果都是7.(1)、请你再选择两个类似的部分试一试,看看是否符合这个规律;(2)、请你利用整式的运算对以上的规律加以证明.
(1)、如图①,点 在直线 两侧,请你在直线 上画出一点 ,使得 的值最小,简述画法、画出图形;(2)、如图②,点 在直线 同侧,请你在直线 上画出一点 ,使得 的值最小,简述画法并画出示意图.21. 一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?(1)、设江水的流速为 千米/时,填空:轮船顺流航行速度为千米/时,逆流航行速度为千米/时,顺流航行100千米所用时间为小时,逆流航行60千米所用时间为小时.(2)、列出方程,并求出问题的解.22. 在日历上,我们可以发现其中某些数满足一定的规律,如图是2012年8月份的日历. 我们任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交叉相乘,再相减,例如: , ,不难发现,结果都是7.(1)、请你再选择两个类似的部分试一试,看看是否符合这个规律;(2)、请你利用整式的运算对以上的规律加以证明.日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
23. 如图所示,直线 交 轴于点 ,交 轴于点 . (1)、如图①,若 的坐标为 ,且 于点 , 交 于点 ,试求点 的坐标;(2)、如图②,在(I)的条件下,连接 ,求 的度数;(3)、如图③,若点 为 的中点,点 为 轴正半轴上一动点,连接 ,过 作 交 轴于 点,当 点在 轴正半轴上运动的过程中,式子 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
(1)、如图①,若 的坐标为 ,且 于点 , 交 于点 ,试求点 的坐标;(2)、如图②,在(I)的条件下,连接 ,求 的度数;(3)、如图③,若点 为 的中点,点 为 轴正半轴上一动点,连接 ,过 作 交 轴于 点,当 点在 轴正半轴上运动的过程中,式子 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.