天津市东丽区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-10 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在△ABC中，AB＝5，AC＝8，则第三边BC的长可能是（）

A、2 B、3 C、6 D、13

查看试题解析
3. 据科学测算，肥皂泡的泡壁厚度大约为0.00071米，数据0.00071用科学记数法表示为（）

A、71×10^﹣⁴ B、0.71×10^﹣⁵ C、7.1×10^﹣⁴ D、71×10^﹣³

查看试题解析
4. 计算（﹣1.5）²⁰¹⁸×（ $\frac{2}{3}$ ）²⁰¹⁹的结果是（）

A、﹣ $\frac{3}{2}$ B、 $\frac{3}{2}$ C、﹣ $\frac{2}{3}$ D、 $\frac{2}{3}$

查看试题解析
5. 解分式方程 $\frac{2}{x - 1} + \frac{x + 2}{1 - x} = 3$ 时，去分母后变形为（）

A、 $2 + (x + 2) = 3 (x - 1)$ B、 $2 - x + 2 = 3 (x - 1)$ C、 $2 - (x + 2) = 3 (1 - x)$ D、 $2 - (x + 2) = 3 (x - 1)$

查看试题解析
6. 如图，已知∠ACD是△ABC的外角，若∠ACD＝135°，∠A＝75°，则∠B的大小为（）

A、60° B、140° C、120° D、90°

查看试题解析
7. 如图，在△ABC中，AB=AC，DE是AC的垂直平分线，△BCD的周长为24，BC=10，则AC等于（）

A、11 B、12 C、14 D、16

查看试题解析
8. 下列计算正确的是（）

A、a³•a⁴＝a¹² B、（﹣2ab²）²＝4a²b⁴ C、（a³）²＝a⁵ D、3a³b²÷a³b²＝3ab

查看试题解析
9. 如图，点B ， F ， C ， E在同一条直线上，点A ， D在直线BE的两侧，AB∥DE ， BF＝CE ，添加一个适当的条件后，仍不能使得△ABC≌△DEF（）

A、AC＝DF B、AC∥DF C、∠A＝∠D D、AB＝DE

查看试题解析
10. 如图， BD 是△ABC 的角平分线， AE⊥ BD ，垂足为 F ．若∠ABC＝35°，∠ C＝50°，则∠CDE 的度数为（）

A、35° B、40° C、45° D、50°

查看试题解析
11. 如图，三角形纸片ABC中，∠B=2∠C，把三角形纸片沿直线AD折叠，点B落在AC边上的E处，那么下列等式成立的是（）

A、AC=AD+BD B、AC=AB+BD C、AC=AD+CD D、AC=AB+CD

查看试题解析
12. 世界文化遗产“三孔”景区已经完成5G基站布设，“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍，在峰值速率下传输500兆数据，5G 网络比4G 网络快45秒，求这两种网络的峰值速率．设4G网络的峰值速率为每秒传输 $x$ 兆数据，依题意，可列方程是（）

A、 $\frac{500}{x} - \frac{500}{10 x} = 45$ B、 $\frac{500}{10 x} - \frac{500}{x} = 45$ C、 $\frac{5000}{x} - \frac{500}{x} = 45$ D、 $\frac{500}{x} - \frac{5000}{x} = 45$

查看试题解析

二、填空题

13. 在平面直角坐标系中，点P（5，﹣3）关于y轴的对称点在第象限．

查看试题解析
14. 分式 $\frac{x - 5}{4 x + 7}$ 有意义，则x的取值范围是．

查看试题解析
15. 若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是．

查看试题解析
16. 若x+y＝4，x²+y²＝6，则xy＝．

查看试题解析
17. 如图，已知△ABC为等边三角形，点D ， E分别在边BC ， AC上，且BD＝CE ，若BE交AD于点F ，则∠AFE的大小为（度）．

查看试题解析
18. 如图，在第一个△A₁BC中，∠B＝30°，A₁B＝CB ，在边A₁B上任取一D ，延长CA₂到A₂ ，使A₁A₂＝A₁D ，得到第2个△A₁A₂D ，在边A₂B上任取一点E ，延长A₁A₂到A₃ ，使A₂A₃＝A₂E ，得到第三个△A₂A₃E ， …按此做法继续下去，第n个等腰三角形的底角的度数是度．

查看试题解析

三、解答题

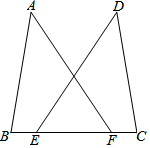
19. 分解因式

(1)、8a³b²+12ab³c

(2)、a³﹣2a²+a

(3)、（2x+y）²﹣（x+2y）²

查看试题解析
20. 计算

(1)、（ $\frac{4}{3}$ xy²﹣2xy）• $\frac{1}{2}$ xy

(2)、[（x+y）•（x﹣y）﹣（x+y）²]÷（﹣2y）

查看试题解析
21. 如图，点 $E$ ， $F$ 在 $B C$ 上， $B E = C F$ ， $A B = D C$ ， $∠ B = ∠ C$ ，求证： $A F = D E$ .

查看试题解析
22. 计算

(1)、 $\frac{4 a}{3 b} \cdot \frac{b}{2 a^{4}} \div {(\frac{1}{a})}^{2}$

(2)、 $\frac{a}{a - 1} \div \frac{a^{2} - a}{a^{2} - 1} - \frac{1}{a - 1}$

查看试题解析
23. 解分式方程

(1)、 $\frac{1}{x - 2} = \frac{1 - x}{2 - x} - 3$

(2)、 $\frac{1}{2 - x} = \frac{1}{x - 2} - \frac{6 - x}{3 x^{2} - 12}$

查看试题解析
24. 2008年5月12日，四川省发生8.0级地震，某市派出两个抢险救灾工程队赶到汶川支援，甲工程队承担了2400米道路抢修任务，乙工程队比甲工程队多承担了600米的道路抢修任务，甲工程队施工速度比乙工程队每小时少修40米，结果两工程队同时完成任务．
问甲、乙两工程队每小时各抢修道路多少米．

(1)、设乙工程队每小时抢修道路x米，则用含x的式子表示：甲工程队每小时抢修道路米，甲工程队完成承担的抢修任务所需时间为小时，乙工程队完成承担的抢修任务所需时间为小时．

(2)、列出方程，完成本题解答．

查看试题解析
25. 如图1，△ABD，△ACE都是等边三角形，

(1)、求证：△ABE≌△ADC；

(2)、若∠ACD=15°，求∠AEB的度数；

(3)、如图2，当△ABD与△ACE的位置发生变化，使C、E、D三点在一条直线上，求证：AC∥BE．

查看试题解析