河北省唐山市丰南区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-10 类型：期末考试

进入出卷网下载

一、单选题

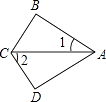
1. 在△ABC中，∠A=20°，∠B=60°，则△ABC的形状是（）

A、等边三角形 B、锐角三角形 C、直角三角形 D、钝角三角形

查看试题解析
2. 数字 $0.00000005$ 用科学记数法表示为（）

A、 $0.5 \times 10^{- 7}$ B、 $0.5 \times 10^{- 8}$ C、 $5 \times 10^{- 7}$ D、 $5 \times 10^{- 8}$

查看试题解析
3. 下列运算正确的是（）

A、 $x^{4} + x^{4} = x^{8}$ B、 $x^{6} ÷ x^{2} = x^{3}$ C、 $x \cdot x^{4} = x^{5}$ D、 ${(x^{2})}^{3} = x^{8}$

查看试题解析
4. 下列分式中，最简分式是（）

A、 $\frac{x^{2} - 1}{x^{2} + 1}$ B、 $\frac{x + 1}{x^{2} - 1}$ C、 $\frac{x^{2} - 2 x y + y^{2}}{x^{2} - x y}$ D、 $\frac{x^{2} - 36}{2 x + 12}$

查看试题解析
5. 利用乘法公式计算正确的是（）

A、（2x﹣3）²=4x²+12x﹣9 B、（4x+1）²=16x²+8x+1 C、（a+b）（a+b）=a²+b² D、（2m+3）（2m﹣3）=4m²﹣3

查看试题解析
6. 如图，∠B=∠D=90°，CB=CD，∠1=30°，则∠2=（）

A、30° B、40° C、50° D、60°

查看试题解析
7. 下列因式分解中：① $x^{3} + 2 x y + x = x (x^{2} + 2 y)$ ；② $- x^{2} + y^{2} = (x + y) (x - y)$ ；③ $x^{2} + 4 x + 4 = {(x + 2)}^{2}$ ；④ $x^{2} + x + 1 = {(x + 1)}^{2}$ ；正确的个数为（）

A、3个 B、2个 C、1个 D、0个

查看试题解析
8. 如图，在 $Δ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B = 15 °$ ， $D E$ 垂直平分 $A B$ ，交 $B C$ 于点 $E$ 若 $B E = 6$ ，则 $A C$ 等于（）

A、3 B、4 C、5 D、6

查看试题解析
9. 若 $3^{x} = 15$ ， $3^{y} = 5$ ，则 $3^{x - y}$ 等于 (　 )

A、5 B、3 C、15 D、10

查看试题解析
10. 某机加工车间共有26名工人，现要加工2100个A零件，1200个B零件，已知每人每天加工A零件30个或B零件20个，问怎样分工才能确保同时完成两种零件的加工任务（每人只能加工一种零件）？设安排x人加工A零件，由题意列方程得（　　）

A、 $\frac{2100}{30 x}$ = $\frac{1200}{20 (26 - x)}$ B、 $\frac{2100}{x}$ = $\frac{1200}{26 - x}$ C、 $\frac{2100}{20 x}$ = $\frac{1200}{30 (26 - x)}$ D、 $\frac{2100}{x}$ ×30= $\frac{1200}{26 - x}$ ×20

查看试题解析
11. 如图，轮船从 $B$ 处以每小时 $50$ 海里的速度沿南偏东 $30 °$ 方向匀速航行，在 $B$ 处观测灯塔 $A$ 位于南偏东 $75 °$ 方向上．轮船航行半小时到达 $C$ 处，在 $C$ 处观测灯塔 $A$ 位于北偏东 $60 °$ 方向上，则 $C$ 处与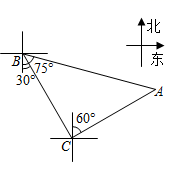灯塔 $A$ 的距离是（）

A、50海里 B、45海里 C、35海里 D、25海里

查看试题解析
12. 老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：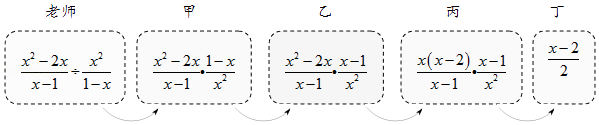
接力中，自己负责的一步出现错误的是（）

A、只有乙 B、甲和丁 C、乙和丙 D、乙和丁

查看试题解析
13. 对于实数 $a$ 、 $b$ ，定义一种新运算“ $\otimes$ ”为： $a \otimes b = \frac{1}{a - b^{2}}$ ，这里等式右边是实数运算．例如： $1 \otimes 3 = \frac{1}{1 - 3^{2}} = - \frac{1}{8}$ ．则方程 $x \otimes (- 2) = \frac{2}{x - 4} - 1$ 的解是（）

A、 $x = 4$ B、 $x = 5$ C、 $x = 6$ D、 $x = 7$

查看试题解析

二、填空题

14. 计算： $x^{2} y^{- 3} {(x^{- 1} y)}^{3} =$ ．

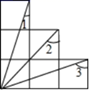
查看试题解析
15. 如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=

查看试题解析
16. 若（x﹣2）^x=1，则x= ．

查看试题解析
17. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $∠ B A C = 100 °$ ， $A B$ 的垂直平分线 $D E$ 分别交 $A B$ ， $B C$ 于点 $D$ ， $E$ ，则 $∠ B A E =$ ．

查看试题解析
18. 若 $a = 2018^{0}$ ， $b = 2017 \times 2019 - 2018^{2}$ ， $c = {(- \frac{4}{5})}^{2017} \times {(\frac{5}{4})}^{2018}$ ，则 $a$ ， $b$ ， $c$ 的大小关系用 $“ <$ "连接为.

查看试题解析
19. 等腰三角形一腰上的高与另一腰的夹角为 $45 °$ ，则其顶角为．

查看试题解析
20. 根据 $(x - 1) (x + 1) = x^{2} - 1$ ， $(x - 1) (x^{2} + x + 1) = x^{3} - 1$ ， $(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$ ， $(x - 1) (x^{4} + x^{3} + x^{2} + x + 1) = x^{5} - 1$ …的规律，则可以得出 $2^{2019} + 2^{2018} + 2^{2017} +$ … $+ 2^{3} + 2^{2} + 2 + 1$ 的末位数字是．

查看试题解析

三、解答题

21.

(1)、计算： $x (x - 2 y) - {(x + y)}^{2}$ ．

(2)、已知 $a + \frac{1}{a} = 5$ ，求 $a - \frac{1}{a}$ 的值．

(3)、化简： $(\frac{x - 2}{x + 2} + \frac{4 x}{x^{2} - 4}) \div \frac{1}{x^{2} - 4}$ ．

查看试题解析
22.

(1)、因式分解： $8 (a^{2} + 1) - 16 a$ ．

(2)、解方程： $\frac{x}{x - 3} - 1 = \frac{1}{x^{2} - 9}$ ．

(3)、先化简： $\frac{x^{2} - 1}{x^{2} - 2 x + 1} \div \frac{x + 1}{x} (x - \frac{1}{x})$ ，然后 $x$ 在 $－ 1$ ， $0$ ， $1$ ， $2$ 四个数中选一个你认为合适的数代入求值．

查看试题解析
23. 已知：如图，AB∥CD，E是AB的中点，CE=DE．求证：

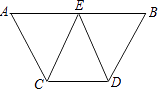(1)、∠AEC=∠BED；

(2)、AC=BD．

查看试题解析
24. 某商场第一次用 $10000$ 元购进某款机器人进行销售，很快销售一空，商家又用 $2400$ 元第二次购进同款机器人，所购进数量是第一次的 $2$ 倍，但单价贵了 $10$ 元．

(1)、求该商家第一次购进机器人多少个？

(2)、若所有机器人都按相同的标价销售，要求全部销售完毕的利润率不低于 $20 % ($ 不考虑其他因素 $)$ ，那么每个机器人的标价至少是多少元？

查看试题解析
25. 如图，在△ABC中，AB＝AC＝2，∠B＝∠C＝40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE＝40°，DE交线段AC于E．

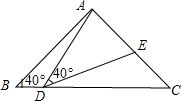(1)、当∠BDA＝115°时，∠EDC＝°，∠DEC＝°；点D从B向C运动时，∠BDA逐渐变（填“大”或“小”）；

(2)、当DC等于多少时，△ABD≌△DCE，请说明理由；

(3)、在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数．若不可以，请说明理由．

查看试题解析