河北省承德市承德县2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-11-10 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x \leq 2$ B、 $x \geq - 2$ C、 $x < - 2$ D、 $x > - 2$

查看试题解析
2. 下列图案中是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 对于 $x + \frac{y}{2}$ ， $\frac{2}{a^{2} + 3}$ ， $\frac{a}{13}$ ， $- \frac{x}{y} + z$ ， $\frac{x (n - 2)}{y}$ ， $\frac{x^{2}}{x}$ ，其中分式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 若 $a < 0$ ，则 $| a - 3 | - \sqrt{a^{2}}$ 的值为（）

A、3 B、-3 C、 $3 - 2 a$ D、 $2 a - 3$

查看试题解析
5. 下列各命题的逆命题是真命题的是（）

A、对顶角相等 B、全等三角形的对应角相等 C、相等的角是同位角 D、等边三角形的三个内角都相等

查看试题解析
6. 如图，已知A ，D，B，E在同一条直线上，且AD = BE， AC = DF，补充下列其中一个条件后，不一定能得到△ABC≌△DEF 的是（）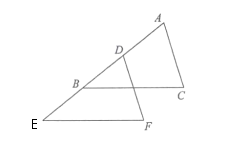

A、BC = EF B、AC//DF C、∠C = ∠F D、∠BAC = ∠EDF

查看试题解析
7. 使分式 $\frac{x^{2} - 4 x - 5}{x + 1}$ 的值等于0的x的值是（）

A、-1 B、-1或5 C、5 D、1或-5

查看试题解析
8. 暑假期间，某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说，第二次购进的数量比第一次多40套，且两次购书时，每套书的进价相同.若设书店第一次购进该科幻小说x套，由题意列方程正确的是（）

A、 $\frac{600}{x} = \frac{800}{x - 40}$ B、 $\frac{600}{x - 40} = \frac{800}{x}$ C、 $\frac{600}{x} = \frac{800}{x + 40}$ D、 $\frac{600}{x + 40} = \frac{800}{x}$

查看试题解析
9. 满足下列条件的是直角三角形的是（）

A、 $B C = 4$ ， $A C = 5$ ， $A B = 6$ B、 $B C = \frac{1}{3}$ ， $A C = \frac{1}{4}$ ， $A B = \frac{1}{5}$ C、 $B C : A C : A B = 3 : 4 : 5$ D、 $∠ A : ∠ B : ∠ C = 3 : 4 : 5$

查看试题解析
10. 如图，在 $Δ A B C$ 中，AB的垂直平分线交AB于点D，交BC于点E． $Δ A B C$ 的周长为19， $Δ A C E$ 的周长为13，则AB的长为（）

A、3 B、6 C、12 D、16

查看试题解析
11. 实数 $a$ 、 $b$ 、 $c$ 、 $d$ 在数轴上的位置如图所示，下列关系式错误的是（）

A、 $| a | > | b |$ B、 $| b - d | = | b | + | d |$ C、 $| a - c | = c - a$ D、 $| d - 1 | > | c - a |$

查看试题解析
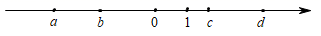12. 如果关于x的方程 $\frac{m}{3 - x} - \frac{1 - x}{x - 3} = 0$ 无解，则m的值是（）

A、2 B、0 C、1 D、–2

查看试题解析
13. 如图，在 $Δ A B C$ ， $∠ C = 90^{\circ}$ ，以 $A$ 为圆心，任意长为半径画弧，分别交 $A C$ ， $A B$ 于点 $M$ ， $N$ ，再分别以 $M$ ， $N$ ，为圆心，大于 $\frac{1}{2} M N$ 长为半径画弧，两弧交于点 $O$ ，作弧线 $A O$ ，交 $B C$ 于点 $E$ ．已知 $C E = 3$ ， $B E = 5$ ，则 $A C$ 的长为（）

A、8 B、7 C、6 D、5

查看试题解析
14. 等腰三角形的一个角比另一个角的 $2$ 倍少 $20$ 度，则等腰三角形顶角的度数是（）

A、 $140^{\circ}$ B、 $20^{\circ}$ 或 $80^{\circ}$ C、 $44^{\circ}$ 或 $80^{\circ}$ D、 $140^{\circ}$ 或 $44^{\circ}$ 或 $80^{\circ}$

查看试题解析
15. 如图， $∠ A C B = 90 °$ ， $A C = C D$ ，过 $D$ 作 $A B$ 的垂线，交 $A B$ 的延长线于 $E$ ，若 $A B = 2 D E$ ，则 $∠ B A C$ 的度数为（）

A、45° B、30° C、22.5° D、15°

查看试题解析
16. 边长为a的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（）

A、 $\frac{1}{3} \times {(\frac{1}{2})}^{5} a$ B、 $\frac{1}{2} \times {(\frac{1}{3})}^{5} a$ C、 $\frac{1}{3} \times {(\frac{1}{2})}^{6} a$ D、 $\frac{1}{2} \times {(\frac{1}{3})}^{6} a$

查看试题解析

二、填空题

17. 如图 $Δ A B C ≅ Δ D C B$ ， $∠ A = 75^{\circ}$ ， $∠ D B C = 40^{\circ}$ ， $∠ D C A$ 则的度数为．

查看试题解析
18. 整体思想就是通过研究问题的整体形式从面对问题进行整体处理的解题方法．如 ${\begin{array}{l} \frac{1}{x} + \frac{1}{y} = 3 \\ \frac{2}{x} + \frac{3}{y} = 7 \end{array}$ ，此题设“ $\frac{1}{x} = a$ ， $\frac{1}{y} = b$ ”，得方程 ${\begin{array}{l} a + b = 3 \\ 2 a + 3 b = 7 \end{array}$ ，解得 ${\begin{array}{l} a = 2 \\ b = 1 \end{array}$ ， $∴ {\begin{array}{l} x = 0.5 \\ y = 1 \end{array}$ ．利用整体思想解决问题：采采家准备装修-厨房，若甲，乙两个装修公司，合做 $6$ 需周完成，甲公司单独做4周后，剩下的由乙公司来做，还需 $9$ 周才能完成，设甲公司单独完成需 $x$ 周，乙公司单独完成需 $y$ 周，则得到方程．利用整体思想，解得．

查看试题解析
19. 在 $Δ A B C$ 中， $A B = A C$ ， $D$ 为直线 $B C$ 上一点， $E$ 为直线 $A C$ 上一点， $A D = A E$ ，设 $∠ B A D = α$ ， $∠ C D E = β$ ．

(1)、如图1，若点 $D$ 在线段 $B C$ 上，点 $E$ 在线段 $A C$ 上，则 $α$ ， $β$ 之间关系式为．

(2)、如图2，若点 $D$ 在线段 $B C$ 上，点 $E$ 在 $C A$ 延长线上，则 $α$ ， $β$ 之间关系式为．

查看试题解析

三、解答题

20. 计算

(1)、 $\sqrt{6} \times \sqrt{2} + \sqrt{24} \div \sqrt{3} - | - 2 \sqrt{3} |$

(2)、 ${(1 - \sqrt{2})}^{0} + {(\frac{1}{2})}^{- 1} - \sqrt{8} \div \sqrt{2} + | \sqrt{2} - 2 |$

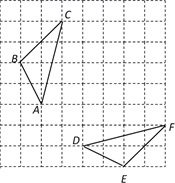
查看试题解析
21. 先化简，再求值： $\frac{a - 2}{a + 1}$ ÷（a﹣1﹣ $\frac{3}{a + 1}$ ），其中a＝ $\sqrt{3}$ ﹣2．

查看试题解析
22. 如图，网格中的△ABC与△DEF为轴对称图形．

(1)、利用网格线作出△ABC与△DEF的对称轴l；

(2)、结合所画图形，在直线l上画出点P，使PA+PC最小；

(3)、如果每一个小正方形的边长为1，请直接写出△ABC的面积= ．

查看试题解析
23. 某县为落实“精准扶贫惠民政策”，计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工，则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天，那么余下的工程由甲队单独完成还需5天.

(1)、这项工程的规定时间是多少天?

(2)、为了缩短工期以减少对居民用水的影响，工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?

查看试题解析
24. 观察下列一组等式，然后解答后面的问题
$(\sqrt{2} + 1) (\sqrt{2} - 1) = 1$ ，

$(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2}) = 1$ ，

$(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3}) = 1$ ，

$(\sqrt{5} + \sqrt{4}) (\sqrt{5} - \sqrt{4}) = 1 \dots \dots$

(1)、观察以上规律，请写出第 $n$ 个等式： $(n$ 为正整数）．

(2)、利用上面的规律，计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{100} + \sqrt{99}}$

(3)、请利用上面的规律，比较 $\sqrt{18} - \sqrt{17}$ 与 $\sqrt{19} - \sqrt{18}$ 的大小．

查看试题解析
25. 如图，在△ABC中，边AB、AC的垂直平分线分别交BC于D、E.

(1)、若BC=5，求△ADE的周长.

(2)、若∠BAD+∠CAE=60°，求∠BAC的度数.

查看试题解析
26. 如图，在 $Δ A B C$ 中， $A B = A C$ ，以 $B C$ 为直角边作等腰 $R t Δ B C D$ ， $∠ C B D = 90^{\circ}$ ，斜边 $C D$ 交 $A B$ 于点 $E$ ．

(1)、如图1，若 $∠ A B C = 60^{\circ}$ ， $B E = 4$ ，作 $E H ⊥ B C$ 于 $H$ ，求线段 $B C$ 的长；

(2)、如图2，作 $C F ⊥ A C$ ，且 $C F = A C$ ，连接 $B F$ ，且 $E$ 为 $A B$ 中点，求证： $C D = 2 B E$ ．

查看试题解析