北京市延庆区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-10 类型:期末考试
一、单选题
-
1. 以下是某中学初二年级的学生在学习了轴对称图形之后设计的.下面这四个图形中,不是轴对称图形的是( )A、
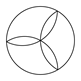 B、
B、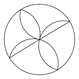 C、
C、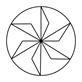 D、
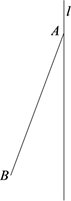
D、 2. 若二次根式 有意义,则 的取值范围是( )A、 B、 C、 D、3. 一个不透明的盒子中装有3个白球、9个红球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的可能性是( )A、 B、 C、 D、4. 下列事件中,属于必然事件的是( )A、任意掷一枚硬币,落地后正面朝上 B、小明妈妈申请北京小客车购买指标,申请后第一次摇号时就中签 C、随机打开电视机,正在播报新闻 D、地球绕着太阳转5. 下列各式中,最简二次根式是( )A、 B、 C、 D、6. 下列运算结果正确的是( )A、 B、 C、 D、7. 如图,数轴上A,B,C,D四点中,与 对应的点距离最近的是( )
2. 若二次根式 有意义,则 的取值范围是( )A、 B、 C、 D、3. 一个不透明的盒子中装有3个白球、9个红球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的可能性是( )A、 B、 C、 D、4. 下列事件中,属于必然事件的是( )A、任意掷一枚硬币,落地后正面朝上 B、小明妈妈申请北京小客车购买指标,申请后第一次摇号时就中签 C、随机打开电视机,正在播报新闻 D、地球绕着太阳转5. 下列各式中,最简二次根式是( )A、 B、 C、 D、6. 下列运算结果正确的是( )A、 B、 C、 D、7. 如图,数轴上A,B,C,D四点中,与 对应的点距离最近的是( ) A、点A B、点B C、点C D、点D8. 如图,D,E分别是AB,AC上的点,BE与CD交于点F,给出下列三个条件:①∠DBF=∠ECF;②∠BDF=∠CEF; ③BD=CE.两两组合在一起,共有三种组合:(1)①②;(2)①③;(3)②③问能判定AB=AC的组合的是( )
A、点A B、点B C、点C D、点D8. 如图,D,E分别是AB,AC上的点,BE与CD交于点F,给出下列三个条件:①∠DBF=∠ECF;②∠BDF=∠CEF; ③BD=CE.两两组合在一起,共有三种组合:(1)①②;(2)①③;(3)②③问能判定AB=AC的组合的是( )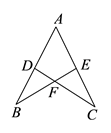 A、(1)(2) B、(1)(3) C、(2)(3) D、(1)(2)(3)
A、(1)(2) B、(1)(3) C、(2)(3) D、(1)(2)(3)二、填空题
-
9. 要使分式 的值为0,则x的值为 .10. 如图,已知AC与BD交于点E,且AB=CD,请你再添加一个边或角的条件使△ABC≌△DCB,添加的条件是: . (添加一个即可)
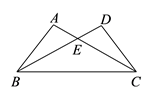 11. 化简: = .12. 如图,EC与DA交于点B,∠ACB=90°,∠A=60°,BD=BE,则∠DEB的度数是.
11. 化简: = .12. 如图,EC与DA交于点B,∠ACB=90°,∠A=60°,BD=BE,则∠DEB的度数是. 13. 为保障冬奥会测试赛顺利进行,北京市延庆区将在2019年年底前基本完成冬奥会有关建设任务,其中之一的内部场馆为圆形设计,面积为 (a,b均为正数)平方米,请你根据所学的知识计算出此场馆内部的半径为米.(用含有a,b的式子表示)14. 如图,在△ABC中,∠A=90°,CD是∠ACB的平分线, DE垂直平分BC,若DE=2,则AB= .
13. 为保障冬奥会测试赛顺利进行,北京市延庆区将在2019年年底前基本完成冬奥会有关建设任务,其中之一的内部场馆为圆形设计,面积为 (a,b均为正数)平方米,请你根据所学的知识计算出此场馆内部的半径为米.(用含有a,b的式子表示)14. 如图,在△ABC中,∠A=90°,CD是∠ACB的平分线, DE垂直平分BC,若DE=2,则AB= .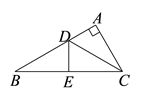 15. 用四个全等的直角三角形拼成如图一个大正方形ABCD和一个小正方形EFGH,这就是著名的“赵爽弦图”.在2002年北京召开的国际数学家大会就用这个弦图作为会标.若AB=10,AF=8,则小正方形EFGH的面积为 .
15. 用四个全等的直角三角形拼成如图一个大正方形ABCD和一个小正方形EFGH,这就是著名的“赵爽弦图”.在2002年北京召开的国际数学家大会就用这个弦图作为会标.若AB=10,AF=8,则小正方形EFGH的面积为 .
 16. 对于任意实数 ,我们规定: .根据上述规定解决下列问题:(1)、计算: .(2)、若 ,则 .
16. 对于任意实数 ,我们规定: .根据上述规定解决下列问题:(1)、计算: .(2)、若 ,则 .三、解答题
-
17. 计算: .18. 计算:(1)、 .(2)、 .19. 如图,点B,F,C,E在直线l上,点A,D在l异侧,AB=DE,AB∥DE,∠A=∠D.求证:△ABC≌△DEF.
 20. 解方程:21. 先化简,再求值 ,其中 .22. 已知,在四边形ABCD中,AB=AD,CB=CD,连接AC,BD.
20. 解方程:21. 先化简,再求值 ,其中 .22. 已知,在四边形ABCD中,AB=AD,CB=CD,连接AC,BD.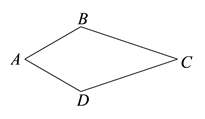 (1)、请补全图形,并说明AC,BD的位置关系;(2)、证明(1)中的结论.23. 小明与小志要到延庆冬奥综合训练馆参加滑冰训练,他们约定从德胜门出发自驾前往,但他们在选择路线时产生了分歧.根据导航提示小明选择方案1前往,小志选择方案2前往,由于方案1比方案2的路线长,而小明还想大家一起到达.已知小明的平均车速比小志的平均车速每小时快8千米,请你帮助小明算一算,他的平均车速为每小时多少千米,他们就可以同时到达?
(1)、请补全图形,并说明AC,BD的位置关系;(2)、证明(1)中的结论.23. 小明与小志要到延庆冬奥综合训练馆参加滑冰训练,他们约定从德胜门出发自驾前往,但他们在选择路线时产生了分歧.根据导航提示小明选择方案1前往,小志选择方案2前往,由于方案1比方案2的路线长,而小明还想大家一起到达.已知小明的平均车速比小志的平均车速每小时快8千米,请你帮助小明算一算,他的平均车速为每小时多少千米,他们就可以同时到达? 24. 已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.
24. 已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.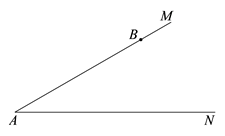 (1)、若△ABC是直角三角形,求AC的长;(2)、若△ABC是等腰三角形,则满足条件的C点有个;(3)、设BC=x,当△ABC唯一确定时,直接写出 的取值范围.25. 动手操作(尺规作图) 已知: 如图线段a,线段b, .求作:△ABC,使得BC=a,∠ABC=α,△ABC的平分线BD=b.
(1)、若△ABC是直角三角形,求AC的长;(2)、若△ABC是等腰三角形,则满足条件的C点有个;(3)、设BC=x,当△ABC唯一确定时,直接写出 的取值范围.25. 动手操作(尺规作图) 已知: 如图线段a,线段b, .求作:△ABC,使得BC=a,∠ABC=α,△ABC的平分线BD=b.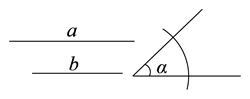 (1)、小园是这样思考的:先画一个草图进行分析,如图1所示,经过分析,小园发现了一个可以确定的三角形 , 确定这个三角形的依据是. 这样基本上就算是完成尺规作图的分析了.(2)、请你用尺规作图法将小园没有做完的完成(在图2中完成即可):
(1)、小园是这样思考的:先画一个草图进行分析,如图1所示,经过分析,小园发现了一个可以确定的三角形 , 确定这个三角形的依据是. 这样基本上就算是完成尺规作图的分析了.(2)、请你用尺规作图法将小园没有做完的完成(在图2中完成即可):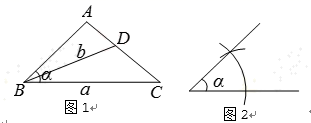 26. 大家都玩过“石头、剪刀、布”的游戏吧?要求参与游戏的人同时做出“石头”、“剪刀”、“布”三种手势中一种,规定:“石头”胜“剪刀”,“剪刀”胜“布”, “布”胜“石头”,若手势相同,则不分胜负.如果两个人做这个游戏,随机出手一次,求两个人获胜的概率各是多少?
26. 大家都玩过“石头、剪刀、布”的游戏吧?要求参与游戏的人同时做出“石头”、“剪刀”、“布”三种手势中一种,规定:“石头”胜“剪刀”,“剪刀”胜“布”, “布”胜“石头”,若手势相同,则不分胜负.如果两个人做这个游戏,随机出手一次,求两个人获胜的概率各是多少?