北京市通州区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-10 类型:期末考试
一、单选题
-
1. 下列手机屏幕解锁图案中,为轴对称图形的是( )A、
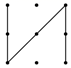 B、
B、 C、
C、 D、
D、 2. 下列实数① ;② ;③ ;④ ,其中是无理数的是( )A、① B、② C、③ D、④3. 若代数式 在实数范围内有意义,则 的取值范围是A、x<1 B、x≤1 C、x>1 D、x≥14. 在元旦联欢会中,抽奖游戏的规则如下:选手蒙眼在一张如图所示的正方形黑白格子纸(九个小正方形面积相等)上描一个点,若所描的点落在黑色区域,获得笔记本一个;若落在白色区域,获得钢笔一支.则选手获得笔记本的概率为( )
2. 下列实数① ;② ;③ ;④ ,其中是无理数的是( )A、① B、② C、③ D、④3. 若代数式 在实数范围内有意义,则 的取值范围是A、x<1 B、x≤1 C、x>1 D、x≥14. 在元旦联欢会中,抽奖游戏的规则如下:选手蒙眼在一张如图所示的正方形黑白格子纸(九个小正方形面积相等)上描一个点,若所描的点落在黑色区域,获得笔记本一个;若落在白色区域,获得钢笔一支.则选手获得笔记本的概率为( ) A、 B、 C、 D、5. 一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )A、至少有1个球是黑球 B、至少有1个球是白球 C、至少有2个球是黑球 D、至少有2个球是白球6. 如图,已知 ,下面甲、乙、丙、丁四个三角形中,与 全等的是( )
A、 B、 C、 D、5. 一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )A、至少有1个球是黑球 B、至少有1个球是白球 C、至少有2个球是黑球 D、至少有2个球是白球6. 如图,已知 ,下面甲、乙、丙、丁四个三角形中,与 全等的是( ) A、甲 B、乙 C、丙 D、丁7. 关于x的分式方程 的解是负数,则m的取值范围是( )A、m>﹣1 B、m>﹣1且m≠0 C、m≥﹣1 D、m≥﹣1且m≠08. 如图, ,点 为射线 上一点,且 ,点 为 的中点.若点 为射线 上一点,则 的最小值为( )
A、甲 B、乙 C、丙 D、丁7. 关于x的分式方程 的解是负数,则m的取值范围是( )A、m>﹣1 B、m>﹣1且m≠0 C、m≥﹣1 D、m≥﹣1且m≠08. 如图, ,点 为射线 上一点,且 ,点 为 的中点.若点 为射线 上一点,则 的最小值为( )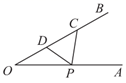 A、2 B、 C、 D、4
A、2 B、 C、 D、4二、填空题
-
9. 请写出一个比2大且比4小的无理数:.10. 若分式 的值等于0,则a的值为 .11. 计算: + = .12. 计算: .13. 若实数a、b满足|a+2|+ =0,则 = .14. 在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有 个.15. 如图,在 中, , , . 平分 交 边于点 ,则 .
 16. 如图, , , .点 , 为线段 上两点.现存在以下条件:① ;② ;③ ;④ .请在以上条件中选择一个条件,使得 一定和 全等,则这个条件可以为 . (请写出所有正确的答案)
16. 如图, , , .点 , 为线段 上两点.现存在以下条件:① ;② ;③ ;④ .请在以上条件中选择一个条件,使得 一定和 全等,则这个条件可以为 . (请写出所有正确的答案)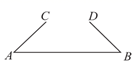
三、解答题
-
17. 如图,在 中, , ,请你按照下面要求完成尺规作图.
①以点 为圆心, 长为半径画弧,交 于点 ,
②再分别以 , 为圆心,大于 的长为半径画弧,两弧交于点 ,
③连接 并延长交 于点 .
请你判断以下结论:
① 是 的一条角平分线;②连接 , 是等边三角形;③ ;
④点 在线段 的垂直平分线上;⑤ .其中正确的结论有(只需要写序号).
 18. 计算: .19. 如图,在 中, , ,点 在 的延长线上,且 ,求 的度数.
18. 计算: .19. 如图,在 中, , ,点 在 的延长线上,且 ,求 的度数.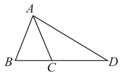 20. 当a=2时,求代数式 的值.21. 解方程: .22. 已知 ,且 交 于点 ,交 于点 , 交 于点 .求证: .
20. 当a=2时,求代数式 的值.21. 解方程: .22. 已知 ,且 交 于点 ,交 于点 , 交 于点 .求证: . 23. 列方程解应用题
23. 列方程解应用题小华和小明两位同学同时为学校元旦联欢会制作彩旗.已知小华每小时比小明多做 面彩旗,小华做 面彩旗与小明做 面彩旗所用时间相等.问小华、小明每小时各做多少面彩旗?
24. 如图,在 中, .点 为 边上一点,线段 将 分为两个周长相等的三角形.若 , ,求 的面积. 25. 我们知道,假分数可以化为带分数.例如: .在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”.例如: , 这样的分式就是假分式; , 这样的分式就是真分式.类似的,假分式也可以化为带分式(即整式与真分式和的形式).
25. 我们知道,假分数可以化为带分数.例如: .在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”.例如: , 这样的分式就是假分式; , 这样的分式就是真分式.类似的,假分式也可以化为带分式(即整式与真分式和的形式).例如:① ;
② .
(1)、将分式 化为带分式;(2)、若分式 的值为整数,求 的整数值;(3)、在代数式 中,若 , 均为整数,请写出 所有可能的取值.26. 如图,在 中, , .点 是射线 上一点,点 是线段 上一点,且点 与点 关于直线 对称,连接 ,过点 作直线 ,垂足为点 ,交 的延长线于点 .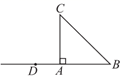 (1)、根据题意完成作图;(2)、请你写出 与 之间的数量关系,并进行证明;(3)、写出线段 , 之间的数量关系,并进行证明.
(1)、根据题意完成作图;(2)、请你写出 与 之间的数量关系,并进行证明;(3)、写出线段 , 之间的数量关系,并进行证明.