北京市顺义区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-10 类型:期末考试
一、单选题
-
1. 如果分式 值为0,那么x的值是( )A、0 B、2 C、-2 D、-2或02. 如图所示,以BC为边的三角形共有( )
 A、1个 B、2个 C、3个 D、4个3. 数轴上, 对应的点在( )
A、1个 B、2个 C、3个 D、4个3. 数轴上, 对应的点在( ) A、点A、B 之间 B、点B与C之间 C、点C与D之间 D、点E与F之间4. 国有银行,是指由国家(财政部、中央汇金公司)直接管控的大型银行.下面是我国其中五个国有银行的图标,分别是中国工商银行、交通银行、中国农业银行、中国银行、中国建设银行,其中轴对称图形有( )
A、点A、B 之间 B、点B与C之间 C、点C与D之间 D、点E与F之间4. 国有银行,是指由国家(财政部、中央汇金公司)直接管控的大型银行.下面是我国其中五个国有银行的图标,分别是中国工商银行、交通银行、中国农业银行、中国银行、中国建设银行,其中轴对称图形有( ) A、2个 B、3个 C、4个 D、5个5. 将 分母有理化的结果为( )A、 B、 C、 D、6. 宏达公司生产了A型、B型两种计算机,它们的台数相同,但总价值和单价不同.已知A型计算机总价值为102万元;B型计算机总价值为81.6万元,且单价比A型机便宜了2400元.问A型、B型两种计算机的单价各是多少万元?对于上述问题用表格分析如下:
A、2个 B、3个 C、4个 D、5个5. 将 分母有理化的结果为( )A、 B、 C、 D、6. 宏达公司生产了A型、B型两种计算机,它们的台数相同,但总价值和单价不同.已知A型计算机总价值为102万元;B型计算机总价值为81.6万元,且单价比A型机便宜了2400元.问A型、B型两种计算机的单价各是多少万元?对于上述问题用表格分析如下:单价/万元
总价/万元
台数/台
A型机
M
B型机
N
如果设A型机单价为x万元,那么B型机单价为(x-0.24)万元.则标记M,N空格中的信息为( )
A、81.6, B、81.6, C、102, D、102,7. 老师组织学生做分组摸球实验.给每组准备了完全相同的实验材料,一个不透明的袋子,袋子中装有除颜色外都相同的3个黄球和若干个白球.先把袋子中的球搅匀后,从中随意摸出一个球,记下球的颜色再放回,即为一次摸球.统计各组实验的结果如下:一组
二组
三组
四组
五组
六组
七组
八组
九组
十组
摸球的次数
100
100
100
100
100
100
100
100
100
100
摸到白球的次数
41
39
40
43
38
39
46
41
42
38
请你估计袋子中白球的个数是( )
A、1个 B、2个 C、3个 D、4个8. 如图,在 △ABC中,AD,AE 分别是 △ABC的角平分线和高线,用等式表示∠DAE、∠B、∠C的关系正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
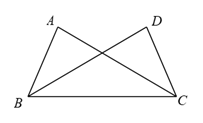
9. 8的平方根是 , 8的立方根是.10. 填空: ,则空为 , .11. 如图, ,那么要得到 ≌ ,可以添加一个条件是(填一个即可), 与 全等的理由是 .
 12. 若 且 ,则 的值为 .13. “任意掷一枚质地均匀的硬币 ,落地后正面朝上”,这个事件是事件.14. 如图,∠C=∠ADB=90°,AD=1,BC= CD=2, 则AB=.
12. 若 且 ,则 的值为 .13. “任意掷一枚质地均匀的硬币 ,落地后正面朝上”,这个事件是事件.14. 如图,∠C=∠ADB=90°,AD=1,BC= CD=2, 则AB=. 15. 为了简洁、明确的表示一个正数的算术平方根,许多数学家进行了探索,期间经历了400余年,直至1637年法国数学家笛卡儿在他的《几何学》中开始使用“ ”表示算数平方根.我国使用根号是由李善兰(1811-1882年)译西方数学书时引用的,她在《代数备旨》中把图1所示题目翻译为: 则图2所示题目(字母代表正数)翻译为 , 计算结果为.
15. 为了简洁、明确的表示一个正数的算术平方根,许多数学家进行了探索,期间经历了400余年,直至1637年法国数学家笛卡儿在他的《几何学》中开始使用“ ”表示算数平方根.我国使用根号是由李善兰(1811-1882年)译西方数学书时引用的,她在《代数备旨》中把图1所示题目翻译为: 则图2所示题目(字母代表正数)翻译为 , 计算结果为. 16. 在 中给定下面几组条件:
16. 在 中给定下面几组条件:①BC=4cm,AC=5cm,∠ACB=30°;
②BC=4cm,AC=3cm,∠ABC=30°;
③BC=4cm,AC=5cm,∠ABC=90°;
④BC=4cm,AC=5cm,∠ABC=120°.
若根据每组条件画图,则 能够唯一确定的是(填序号).
三、解答题
-
17. 已知:如图,AC=BD,AC∥BD,AB和CD相交于点O.求证: ≌ .
 18. 计算: .19. 计算:20. 计算: .21. 学习了分式运算后,老师布置了这样一道计算题: ,下面是一位同学有错的解答过程:
18. 计算: .19. 计算:20. 计算: .21. 学习了分式运算后,老师布置了这样一道计算题: ,下面是一位同学有错的解答过程: (1)、该同学的解答过程的错误步骤是;(填序号)你认为该同学错误的原因是 .(2)、请写出正确解答过程.22. 下面是小明同学设计的“作一个角等于已知角”的尺规作图过程.
(1)、该同学的解答过程的错误步骤是;(填序号)你认为该同学错误的原因是 .(2)、请写出正确解答过程.22. 下面是小明同学设计的“作一个角等于已知角”的尺规作图过程.已知:∠O,
求作:一个角,使它等于∠O.
作法:如图:


①在∠O的两边上分别任取一点A,B;
②以点A为圆心,OA为半径画弧;以点B为
圆心,OB为半径画弧;两弧交于点C;
③连结AC,BC ,所以∠C即为所求作的角.
请根据小明设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下列证明.证明:连结AB,
∵OA=AC,OB= , ,
∴ ≌ ()(填推理依据).
∴∠C=∠O.
23. 解方程: .24. 求 的值,其中 .25. 如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证:BD=CE.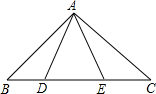 26. 为了解某校八年级全体女生“仰卧起坐”项目的成绩,随机抽取了部分女生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制成如下不完整的统计图、表.
26. 为了解某校八年级全体女生“仰卧起坐”项目的成绩,随机抽取了部分女生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制成如下不完整的统计图、表.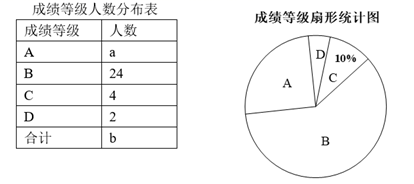
根据以上信息解答下列问题:
(1)、a= , b= , 表示A等级扇形的圆心角的度数为度;(2)、A等级中有八年级(5)班两名学生,如果要从A等级学生中随机选取一名介绍“仰卧起坐”锻炼经验,求抽到八年级(5)班学生的可能性大小.27. 在平面内,给定∠AOB=60°,及OB边上一点C,如图所示.到射线OA,OB距离相等的所有点组成图形G,线段OC的垂直平分线交图形G于点D,连接CD.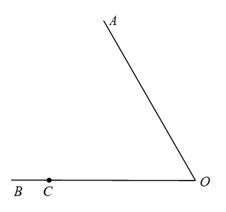 (1)、依题意补全图形;直接写出∠DCO的度数;(2)、过点D作OD的垂线,交OA于点E,OB于点F.求证:CF=DE.28. 现代科技的发展已经进入到了5G时代,“5G”即第五代移动通信技术(英语:5th generation mobile networks或5th generation wireless systems、5th-Generation,简称5G或5G技术)是最新一代蜂窝移动通信技术,也是即4G(LTE-A、WiMax)、3G(UMTS、LTE)和2G(GSM)系统之后的延伸。中国信息通信科技集团有限公司工程师余少华院士说“同4G相比,5G的传输速率提高了10至100倍.”“从人人互联、人物互联,到物物互联,再到人网物三者的结合,5G技术最终将构建起万物互联的智能世界” 如果5G网络峰值速率是4G网络峰值速率的10倍,那么在峰值速率下传输1 000MB数据,5G网络比4G网络快90秒,求这两种网络的峰值速率(MB/秒).29. 如图,在Rt 中,∠C=90°,AC=BC,在线段CB延长线上取一点P,以AP为直角边,点P为直角顶点,在射线CB上方作等腰 Rt , 过点D作DE⊥CB,垂足为点E.
(1)、依题意补全图形;直接写出∠DCO的度数;(2)、过点D作OD的垂线,交OA于点E,OB于点F.求证:CF=DE.28. 现代科技的发展已经进入到了5G时代,“5G”即第五代移动通信技术(英语:5th generation mobile networks或5th generation wireless systems、5th-Generation,简称5G或5G技术)是最新一代蜂窝移动通信技术,也是即4G(LTE-A、WiMax)、3G(UMTS、LTE)和2G(GSM)系统之后的延伸。中国信息通信科技集团有限公司工程师余少华院士说“同4G相比,5G的传输速率提高了10至100倍.”“从人人互联、人物互联,到物物互联,再到人网物三者的结合,5G技术最终将构建起万物互联的智能世界” 如果5G网络峰值速率是4G网络峰值速率的10倍,那么在峰值速率下传输1 000MB数据,5G网络比4G网络快90秒,求这两种网络的峰值速率(MB/秒).29. 如图,在Rt 中,∠C=90°,AC=BC,在线段CB延长线上取一点P,以AP为直角边,点P为直角顶点,在射线CB上方作等腰 Rt , 过点D作DE⊥CB,垂足为点E. (1)、依题意补全图形;(2)、求证: AC=PE;(3)、连接DB,并延长交AC的延长线于点F,用等式表示线段CF与AC的数量关系,并证明.30. A表示一个数,若把数A写成形如 的形式,其中 、 、 、 、…都为整数.则我们称把数A写成连分数形式.
(1)、依题意补全图形;(2)、求证: AC=PE;(3)、连接DB,并延长交AC的延长线于点F,用等式表示线段CF与AC的数量关系,并证明.30. A表示一个数,若把数A写成形如 的形式,其中 、 、 、 、…都为整数.则我们称把数A写成连分数形式.例如:把2.8写成连分数形式的过程如下:
2.8-2=0.8, ,
1.25-1=0.25, ,
4-4=0.
(1)、把3.245写成连分数形式不完整的过程如下:3.245-3=0.245, ,
4.082-4=0.082, ,
12.250-12=0.25, ,
4-4=0.
∴
则 ; ;
(2)、请把 写成连分数形式;(3)、有这样一个问题:如图是长为47,宽为10的长方形纸片.从中裁剪出正方形,若长方形纸片无剩余,则剪出的正方形最少是几个?
小明认为这个问题和 “把一个数化为连分数形式” 有关联,并把 化成连分数从而解决了问题.你可以参考小明的思路解决上述问题,请直接写出“剪出的正方形最少”时,正方形的个数.